Métaanalyse avec R : Différence entre versions
| (12 révisions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 56 : | Ligne 56 : | ||
Cette grandeur est nécessaire pour comparer les différentes études, et le but de la méta-analyse est précisément d'en obtenir une valeur corrigée. <br /> | Cette grandeur est nécessaire pour comparer les différentes études, et le but de la méta-analyse est précisément d'en obtenir une valeur corrigée. <br /> | ||
| − | Il est de convention d’assumer la normalité des | + | Il est de convention d’assumer la normalité des grandeurs d'effets ; ce qui n'est pas abusif à partir du moment où l’échantillon est de taille suffisante (application du Théorème Central Limite). Pour normaliser les grandeurs d'effet il est usuel d’utiliser une transformation logarithmique. ([http://www.edii.uclm.es/~useR-2013/Tutorials/kovalchik/kovalchik_meta_tutorial.pdf Tutorial: Performing Meta-Analysis With R - Stephanie A. Kovalchik, National Cancer Institute]) |
==== A partir des observations (fonction escalc) ==== | ==== A partir des observations (fonction escalc) ==== | ||
Dans le package metafor, la fonction escalc permet de calculer directement les logESs et les variances correspondantes (SElogES<sup>2</sup>) à partir du nombre d'individus observés (tableau). | Dans le package metafor, la fonction escalc permet de calculer directement les logESs et les variances correspondantes (SElogES<sup>2</sup>) à partir du nombre d'individus observés (tableau). | ||
| − | ''(Pour la suite on prendra l'exemple des Odd Ratios)'' | + | Il est important de noter qu'il s'agit bien de la variance du logarithme de l'ES, et non de l'ES directement ! (la formulation utilisée dans certaines sources de documentation peuvent parfois porter à confusion là dessus). |
| + | |||
| + | ''(Pour la suite on prendra l'exemple des Odd Ratios comme effect size)'' | ||
<pre> | <pre> | ||
### calculate log odds ratios and corresponding sampling variances | ### calculate log odds ratios and corresponding sampling variances | ||
| Ligne 72 : | Ligne 74 : | ||
==== A partir des données brutes ==== | ==== A partir des données brutes ==== | ||
| − | Si les données recueuillies sur les études sont déjà des Odd ratio, il est possible de retrouver ces grandeurs | + | Si les données recueuillies sur les études sont déjà des Odd ratio, il est possible de retrouver ces grandeurs à l'aide de l'intervalle de confiance de l'OR (à 95%) |
| − | + | ||
| − | + | <math>\begin{align} IC(OR)=[a,b] \\ | |
| − | + | ||
| − | + | \Rightarrow IC(lnOR)=[lna,lnb] \\ | |
| − | + | \\ | |
| + | Comme lnOR \longrightarrow \mathcal{N}(\mu,SElnOR^2) \\ | ||
| + | IC(lnOR)=[\mu \pm 1,96 \times SElnOR] \\ | ||
| + | \\ | ||
| + | Resoudre : \left\{ | ||
| + | \begin{array}{l} | ||
| + | \mu - 1,96 \times SElnOR = lna \\ | ||
| + | \mu + 1,96 \times SElnOR = lnb | ||
| + | \end{array} | ||
| + | \right. \\ | ||
| + | |||
| + | \Rightarrow \left\{ | ||
| + | \begin{array}{l} | ||
| + | \mu = \frac{ln(a \times b)}{2} \\ | ||
| + | SElnOR = \frac{ln(\frac{a}{b})}{2\times 1,96} | ||
| + | \end{array} | ||
| + | \right. \\ | ||
| + | \end{align} | ||
| + | </math><br /> | ||
| + | <br /> | ||
| + | |||
| + | |||
| + | Autre méthode envisageable et plus simple ? <big>'''(A discuter !)'''</big> | ||
| + | On utilise : | ||
| + | |||
| + | |||
| + | <math> | ||
| + | \begin{align} | ||
| + | |||
| + | lna = lnOR - 1,96 \times SElnOR \\ | ||
| + | \Rightarrow SElnOR = \frac{lnOR - lna}{1,96} \\ | ||
| + | \end{align} | ||
| + | </math> | ||
=== Méta-analyse === | === Méta-analyse === | ||
| + | |||
Plusieurs fonctions sont disponibles dans le package metafor, voir la documentation du package pour plus de détails. | Plusieurs fonctions sont disponibles dans le package metafor, voir la documentation du package pour plus de détails. | ||
| − | |||
Deux fonctions intéressantes : | Deux fonctions intéressantes : | ||
| + | * rma.uni | ||
| + | * rma.mv | ||
==== rma.uni (Random effect Meta-Analysis) ==== | ==== rma.uni (Random effect Meta-Analysis) ==== | ||
| Ligne 92 : | Ligne 128 : | ||
Par défaut la méthode utilisée est RE REML (Random Effect avec REstricted Maximum Likehood). | Par défaut la méthode utilisée est RE REML (Random Effect avec REstricted Maximum Likehood). | ||
| + | Pour la suite, on renomme alpha les lnOR, et beta la variance correspondante (soit SElnOR<sup>2</sup>) | ||
| + | <pre> | ||
| + | #Alpha=LnOR | ||
| + | #Beta=VarLnOR | ||
| + | dat$alpha<-dat$yi | ||
| + | dat$beta<-dat$vi</pre> | ||
'''exemple 1 : Première régression, sans inclure de modérateurs dans le modèle :''' | '''exemple 1 : Première régression, sans inclure de modérateurs dans le modèle :''' | ||
<pre>### random-effects model using rma.uni() | <pre>### random-effects model using rma.uni() | ||
| − | resrma<-rma.uni(yi, vi, measure="OR", data=dat) | + | resrma<-rma.uni(yi=alpha, vi=beta, measure="OR",data=dat) |
resrma$b #lnOR=-0.745 | resrma$b #lnOR=-0.745 | ||
| Ligne 110 : | Ligne 152 : | ||
* method : permet de spécifier un modèle à effets fixes par exemple. | * method : permet de spécifier un modèle à effets fixes par exemple. | ||
| + | <br /> | ||
| + | <big>'''Il est important de noter que dans toutes les fonctions utilisées, les arguments requis (yi et vi) sont les effect size normalisés (que l'on a renommé précédemment alpha et beta), même si l'argument "measure" indique "OR"''' | ||
| + | </big> | ||
| + | <br /> | ||
[[Fichier:without_moderators.png]] | [[Fichier:without_moderators.png]] | ||
| Ligne 116 : | Ligne 162 : | ||
'''exemple 2 : fixed effect modèle''' | '''exemple 2 : fixed effect modèle''' | ||
<pre>### fixed-effects model using rma.uni() | <pre>### fixed-effects model using rma.uni() | ||
| − | resfe<-rma.uni(yi= | + | resfe<-rma.uni(yi=alpha, vi=beta, measure="OR",data=dat, method="FE") |
resfe | resfe | ||
resfe$b #lnOR=-0.4361 | resfe$b #lnOR=-0.4361 | ||
| Ligne 122 : | Ligne 168 : | ||
</pre> | </pre> | ||
| − | [[Fichier: | + | |
| + | [[Fichier:fixed_effect.png]] | ||
| + | |||
| + | |||
On peut vouloir inclure des covariates dans le modèle, devant la forte hétérogénéité observée observée entre les études (I<sup>2</sup>=99.92%) | On peut vouloir inclure des covariates dans le modèle, devant la forte hétérogénéité observée observée entre les études (I<sup>2</sup>=99.92%) | ||
| Ligne 128 : | Ligne 177 : | ||
'''exemple 3 : metaregression avec une seule variable :''' | '''exemple 3 : metaregression avec une seule variable :''' | ||
<pre>### Meta-regression incluant la variable latitude | <pre>### Meta-regression incluant la variable latitude | ||
| − | res.lat<-rma.uni(yi= | + | res.lat<-rma.uni(yi=alpha, vi=beta, measure="OR",data=dat, mods =ablat) |
res.lat | res.lat | ||
| Ligne 137 : | Ligne 186 : | ||
(resrma$I2-res.lat$I2)/resrma$I2 #Baisse de l'hétérogénéité de 42.6% | (resrma$I2-res.lat$I2)/resrma$I2 #Baisse de l'hétérogénéité de 42.6% | ||
</pre> | </pre> | ||
| + | |||
| + | |||
| + | [[Fichier:Meta_unmoderator.png]] | ||
'''exemple 4 : metaregression incluant les trois variables explicatives :''' | '''exemple 4 : metaregression incluant les trois variables explicatives :''' | ||
<pre>### Meta-regression incluant les variables latitude, année et allocation du traitement | <pre>### Meta-regression incluant les variables latitude, année et allocation du traitement | ||
| − | res.meta<-rma.uni(yi= | + | res.meta<-rma.uni(yi=alpha, vi=beta, measure="OR",data=dat, mods = ~ ablat + factor(alloc) + year ) |
res.meta | res.meta | ||
</pre> | </pre> | ||
| + | |||
| + | [[Fichier:meta_troismoderators.png]] | ||
| Ligne 149 : | Ligne 203 : | ||
Présente l’avantage d’offrir la possibilité de préciser la structure de la corrélation entre les publications (par exemple issues d’une même étude), via les arguments ''struct'' et ''random''. | Présente l’avantage d’offrir la possibilité de préciser la structure de la corrélation entre les publications (par exemple issues d’une même étude), via les arguments ''struct'' et ''random''. | ||
| − | rma.mv(yi, | + | '''exemple : données BCG''' |
| − | + | Dans l’exemple, on considère que chaque essai est composée de deux études différentes : une sur la population vaccinée et l’autre sur la population de contrôle. Dans chaque cas, on observe le nombre d’individus atteints ou non par la tuberculose (les variables sont respectivement out1 et out2). | |
| − | + | ||
| + | <pre>### bivariate random-effects model using rma.mv() | ||
| + | |||
| + | ### change data into long format | ||
| + | dat.long <- to.long(measure="OR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat.bcg) | ||
| + | #chaque étude divisée en deux : vaccinés (group=1) ou non (group=2) | ||
| + | #out1=nb d'individus atteints | ||
| + | #out2=nb non atteints | ||
| + | |||
| + | ### calculate log odd-ratios and corresponding sampling variances | ||
| + | dat.long <- escalc(measure="PLO", xi=out1, mi=out2, data=dat.long) | ||
| + | #yi=ln(out1/out2) | ||
| + | |||
| + | ### set "2" (controlled/non-vaccinated) to reference level of group variable | ||
| + | dat.long$group <- relevel(dat.long$group, ref=2) | ||
| + | </pre> | ||
| + | |||
| + | De nouveau, on renomme alpha et beta respectivement les effect size normalisés et leur variance. | ||
| + | <pre> | ||
| + | #Alpha=LnOR | ||
| + | #Beta=VarLnOR | ||
| + | dat.long$alpha<-dat.long$yi | ||
| + | dat.long$beta<-dat.long$vi | ||
| + | |||
| + | ### bivariate random-effects model using rma.mv() | ||
| + | res <- rma.mv(yi=alpha, vi=beta, mods = ~ group, random = ~ group | study, struct="UN", method="REML", data=dat.long) | ||
| + | res</pre> | ||
| − | method : Restricted Maximum Likehood semble être | + | avec : |
| + | * xi : nombre d’observations de l’évènement observé (ici la tuberculose) | ||
| + | * mi : nombre d’observations de l’évènement complémentaire | ||
| + | ici : yi = ln(out1/out2) | ||
| + | method : de nouveau : fixed or random-effect model, différentes méthodes d’estimation pour tau2. | ||
| + | A noter que la méthode du Restricted Maximum Likehood semble être la plus performante. | ||
| + | * random : permet de spécifier la structure du "random effect" du modèle : | ||
| + | ~ inner | outer (un seul possible) : les outcomes avec des niveaux différents de la variable outer sont considérés indépendants tandis que les outcomes avec un niveau identique de la variable outer sont corrélés suivant un "random effect" correspondant au niveaux de la variable inner. <br /> | ||
| + | ~ 1 | id. Random effect sur la variable "id" : les outcomes avec des niveaux différents de la variable id sont considérés indépendants, mais pas si le niveau est le même (par exemple si les essais proviennent d'une même étude). | ||
| + | * struct : permet de spécifier la structure de la variance indiquée dans l'argument random ("UN" pour unstructured variance- covariance matrix). | ||
| + | <br /> | ||
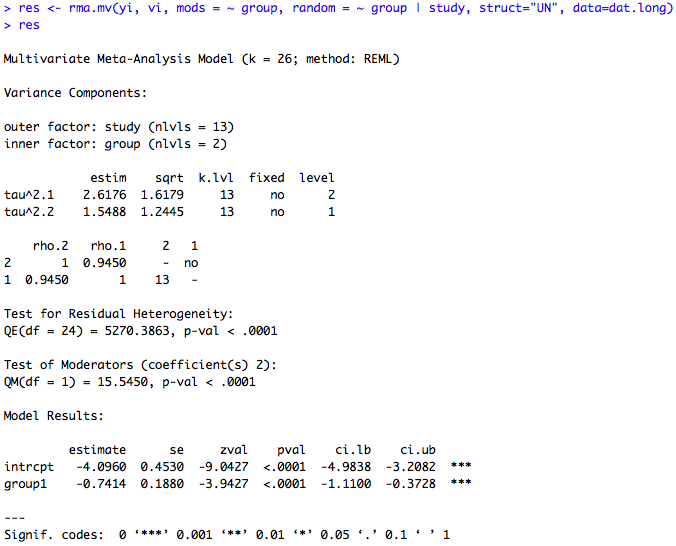
| + | ''Sortie R :'' | ||
| + | [[Fichier:meta.rmamv.png]] | ||
Version actuelle datée du 18 juillet 2014 à 10:11
Sommaire
Objectifs
La méta-analyse est une méthode statistique qui fût inventée en 1904 par Karl Pearson pour tenter de surmonter le problème de puissance statistique réduite dans les études d'échantillons de petites tailles. Aujourd'hui, elle est très utilisée dans le domaine de la santé, où les chercheurs sont confrontés à la multiplicité d'études et d'essais thérapeutiques portant sur un même sujet, mais dont les protocoles mis en place et plus généralement les conditions des études diffèrent. En effet, la méta-analyse consiste en une synthèse quantitative de ces différents résultats pour obtenir une valeur "corrigée" qui intègre plus d'informations qu'une valeur unique prise dans la littérature (avec plus ou moins de justifications) ou bien qu'une simple moyenne des valeurs de la littérature.
Dans un premier temps, il s'agit donc de collecter les valeurs de résultats des essais déjà réalisés, ainsi que les conditions dans lesquelles ils ont été obtenus. Pour celà, il est donc nécessaire de définir au préalable des critères d'inclusion ou non des études qui soient précisément établis. A noter que cette recherche doit être la plus exhaustive possible afin que la méta-analyse soit une synthèse pertinente de la littérature existante sur le sujet défini.
Package METAFOR
Il existe trois packages dans R permettant de réaliser des méta-analyses : META, RMETA et METAFOR. Ce dernier est cependant le plus perfectionné puisqu’il offre la possibilité de réaliser des méta-régressions, d’utiliser un modèle à effets fixes ou bien aléatoires, ou encore car il intègre le calcul de différentes mesures d’hétérogénéité.
Pour la suite, on prend l’exemple d’un traitement binaire (succès : Y=1 ou échec : Y=0). appliqué à une population test (X=1) mais pas à une population de contrôle (X=0).
A noter que X peut aussi être l'exposition à une maladie.
Jeu de données BCG
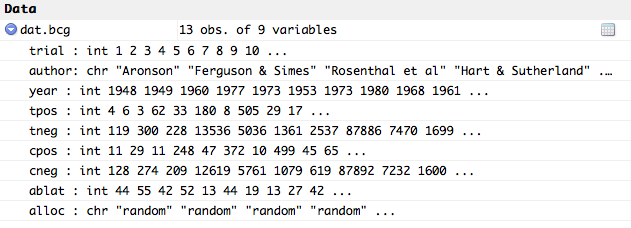
Pour illustrer, on utilisera le jeu de données « BCG » du package metafor.qui contient les données de 13 essais cliniques du vaccin Bacillus Calmette–Guérin (BCG). Ainsi, le traitement (variable X) consiste en l'administration ou non du vaccin, et la variable observée (Y) est l'infection ou non par la tuberculose. Les données contiennent également trois variables explicatives possibles :
- l'année de publication
- la latitude de la région où s'est déroulé l'essai
- la méthode d'allocation du traitement choisie pour l'essai.
#metafor package library(metafor) ### load BCG vaccine data data(dat.bcg)
Les résultats d’un essai peuvent être représentés sous la forme suivante :
| vacciné | non vacciné | Total individus | |
|---|---|---|---|
| Tuberculeux | a = tpos | c = cpos | n1 |
| Non tuberculeux | b = tneg | d = cneg | n2 |
Calcul de la taille d'effet ("effect size")
Par exemple : Odd ratio, Risque Relatif, Ecart de moyenne,..
Cette grandeur est nécessaire pour comparer les différentes études, et le but de la méta-analyse est précisément d'en obtenir une valeur corrigée.
Il est de convention d’assumer la normalité des grandeurs d'effets ; ce qui n'est pas abusif à partir du moment où l’échantillon est de taille suffisante (application du Théorème Central Limite). Pour normaliser les grandeurs d'effet il est usuel d’utiliser une transformation logarithmique. (Tutorial: Performing Meta-Analysis With R - Stephanie A. Kovalchik, National Cancer Institute)
A partir des observations (fonction escalc)
Dans le package metafor, la fonction escalc permet de calculer directement les logESs et les variances correspondantes (SElogES2) à partir du nombre d'individus observés (tableau). Il est important de noter qu'il s'agit bien de la variance du logarithme de l'ES, et non de l'ES directement ! (la formulation utilisée dans certaines sources de documentation peuvent parfois porter à confusion là dessus).
(Pour la suite on prendra l'exemple des Odd Ratios comme effect size)
### calculate log odds ratios and corresponding sampling variances dat <- escalc(measure="OR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat.bcg) cbind(dat$yi,dat$vi)
A partir des données brutes
Si les données recueuillies sur les études sont déjà des Odd ratio, il est possible de retrouver ces grandeurs à l'aide de l'intervalle de confiance de l'OR (à 95%)
<math>\begin{align} IC(OR)=[a,b] \\
\Rightarrow IC(lnOR)=[lna,lnb] \\ \\ Comme lnOR \longrightarrow \mathcal{N}(\mu,SElnOR^2) \\ IC(lnOR)=[\mu \pm 1,96 \times SElnOR] \\ \\ Resoudre : \left\{ \begin{array}{l}
\mu - 1,96 \times SElnOR = lna \\ \mu + 1,96 \times SElnOR = lnb
\end{array} \right. \\
\Rightarrow \left\{ \begin{array}{l}
\mu = \frac{ln(a \times b)}{2} \\
SElnOR = \frac{ln(\frac{a}{b})}{2\times 1,96}
\end{array}
\right. \\
\end{align}
</math>
Autre méthode envisageable et plus simple ? (A discuter !)
On utilise :
<math>
\begin{align}
lna = lnOR - 1,96 \times SElnOR \\ \Rightarrow SElnOR = \frac{lnOR - lna}{1,96} \\ \end{align} </math>
Méta-analyse
Plusieurs fonctions sont disponibles dans le package metafor, voir la documentation du package pour plus de détails. Deux fonctions intéressantes :
- rma.uni
- rma.mv
rma.uni (Random effect Meta-Analysis)
Permet de réaliser des méta-analyses avec un modèle linéaire :
- à effets fixes ou mixed/random
- avec ou sans modérateurs
Par défaut la méthode utilisée est RE REML (Random Effect avec REstricted Maximum Likehood).
Pour la suite, on renomme alpha les lnOR, et beta la variance correspondante (soit SElnOR2)
#Alpha=LnOR #Beta=VarLnOR dat$alpha<-dat$yi dat$beta<-dat$vi
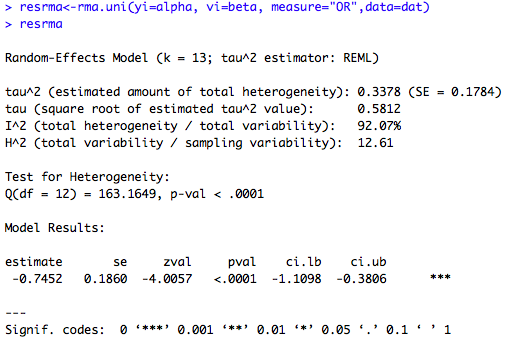
exemple 1 : Première régression, sans inclure de modérateurs dans le modèle :
### random-effects model using rma.uni() resrma<-rma.uni(yi=alpha, vi=beta, measure="OR",data=dat) resrma$b #lnOR=-0.745 exp(-0.745) #OR corrigé = 0.4747
avec :
- yi : vecteur de longueur k (le nombre d’études) des lnOR observés (ou plus généralement les outcomes normalisés)
- vi (ou sei) : vecteur de longueur k contenant les variances (ou standard errors) correspondantes.
Plusieurs arguments peuvent être ajoutés :
- mods : permet d’inclure un ou plusieurs modérateurs dans le modèle.
- weights : par défaut le poids donné à chaque étude dans l’analyse est égal à l’inverse de sa variance, mais il peut être spécifié.
- method : permet de spécifier un modèle à effets fixes par exemple.
Il est important de noter que dans toutes les fonctions utilisées, les arguments requis (yi et vi) sont les effect size normalisés (que l'on a renommé précédemment alpha et beta), même si l'argument "measure" indique "OR"
exemple 2 : fixed effect modèle
### fixed-effects model using rma.uni() resfe<-rma.uni(yi=alpha, vi=beta, measure="OR",data=dat, method="FE") resfe resfe$b #lnOR=-0.4361 exp(-0.4361) #OR corrigé = 0.6465531
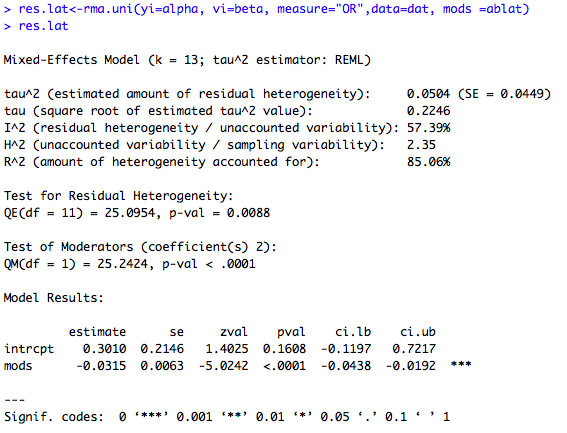
On peut vouloir inclure des covariates dans le modèle, devant la forte hétérogénéité observée observée entre les études (I2=99.92%)
exemple 3 : metaregression avec une seule variable :
### Meta-regression incluant la variable latitude res.lat<-rma.uni(yi=alpha, vi=beta, measure="OR",data=dat, mods =ablat) res.lat #Comparaison des résultats : exp(c(resrma$b, res.lat$b[1])) #OR corrigé : 0.4587 vs. 1.3513 c(resrma$I2, res.lat$I2) #I^2 (resrma$I2-res.lat$I2)/resrma$I2 #Baisse de l'hétérogénéité de 42.6%
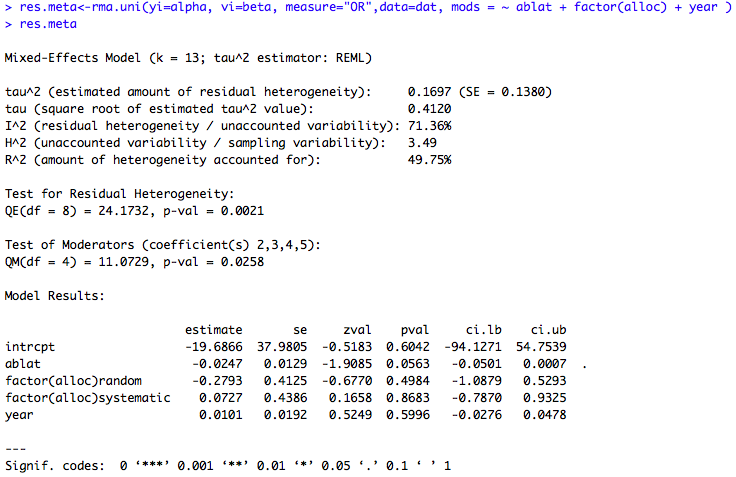
exemple 4 : metaregression incluant les trois variables explicatives :
### Meta-regression incluant les variables latitude, année et allocation du traitement res.meta<-rma.uni(yi=alpha, vi=beta, measure="OR",data=dat, mods = ~ ablat + factor(alloc) + year ) res.meta
rma.mv (Random effect Meta-Analysis via Multivariate/Multilevel Linear Models
Présente l’avantage d’offrir la possibilité de préciser la structure de la corrélation entre les publications (par exemple issues d’une même étude), via les arguments struct et random.
exemple : données BCG Dans l’exemple, on considère que chaque essai est composée de deux études différentes : une sur la population vaccinée et l’autre sur la population de contrôle. Dans chaque cas, on observe le nombre d’individus atteints ou non par la tuberculose (les variables sont respectivement out1 et out2).
### bivariate random-effects model using rma.mv() ### change data into long format dat.long <- to.long(measure="OR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat.bcg) #chaque étude divisée en deux : vaccinés (group=1) ou non (group=2) #out1=nb d'individus atteints #out2=nb non atteints ### calculate log odd-ratios and corresponding sampling variances dat.long <- escalc(measure="PLO", xi=out1, mi=out2, data=dat.long) #yi=ln(out1/out2) ### set "2" (controlled/non-vaccinated) to reference level of group variable dat.long$group <- relevel(dat.long$group, ref=2)
De nouveau, on renomme alpha et beta respectivement les effect size normalisés et leur variance.
#Alpha=LnOR #Beta=VarLnOR dat.long$alpha<-dat.long$yi dat.long$beta<-dat.long$vi ### bivariate random-effects model using rma.mv() res <- rma.mv(yi=alpha, vi=beta, mods = ~ group, random = ~ group | study, struct="UN", method="REML", data=dat.long) res
avec :
- xi : nombre d’observations de l’évènement observé (ici la tuberculose)
- mi : nombre d’observations de l’évènement complémentaire
ici : yi = ln(out1/out2) method : de nouveau : fixed or random-effect model, différentes méthodes d’estimation pour tau2. A noter que la méthode du Restricted Maximum Likehood semble être la plus performante.
- random : permet de spécifier la structure du "random effect" du modèle :
~ inner | outer (un seul possible) : les outcomes avec des niveaux différents de la variable outer sont considérés indépendants tandis que les outcomes avec un niveau identique de la variable outer sont corrélés suivant un "random effect" correspondant au niveaux de la variable inner.
~ 1 | id. Random effect sur la variable "id" : les outcomes avec des niveaux différents de la variable id sont considérés indépendants, mais pas si le niveau est le même (par exemple si les essais proviennent d'une même étude).
- struct : permet de spécifier la structure de la variance indiquée dans l'argument random ("UN" pour unstructured variance- covariance matrix).