Regression linéaire avec R : Différence entre versions
(→Regression linéaire simple) |
|||
| (Une révision intermédiaire par le même utilisateur non affichée) | |||
| Ligne 58 : | Ligne 58 : | ||
[[Fichier:droitereg.png]] | [[Fichier:droitereg.png]] | ||
| − | |||
=== Regression linéaire multiple === | === Regression linéaire multiple === | ||
Version actuelle datée du 24 janvier 2019 à 15:28
Données
Pour illustrer, on utilise le jeu de données « housingprices » (issu du package DAAG), composé de quinze observations et trois variables :
- sale.price = prix de vente de la maison (en milliers de dollars australiens)
- area = surface au sol de la maison
- bedrooms = nombre de chambres dans la maison
#### Installe + charge le package DAAG
install.packages("DAAG")
library(DAAG)
### Charge les données
data(houseprices)
### Aperçu des premières lignes
head(houseprices)
Objectif
On peut vouloir expliquer le prix de vente des maisons, en fonction de leur surface en présumant que plus la surface est élevée, et plus le prix de vente sera élevé. Il s'agit là d'une regression dite "simple" car elle ne comporte qu'une seule variables explicative. De plus, on peut aussi supposer que le nombre de chambres influence le prix de la maison à la hausse ; il s'agira là d'une regression "multiple" avec deux variables explicatives.
L’objectif est d’évaluer si chacune des deux variables influence le prix, et, si tel est le cas, de tenter de quantifier cet effet.
La regression linéaire
La regression linéaire assume que la relation entre les variables explicatives et la variable à expliquer (variable numérique continue) va être linéaire, du type : <math>y_{i} = b0 + b1 \times x1_{i} + b2 \times x2_{i} + e_{i} </math>
où :
- y est la variable à expliquer (ici : sale.price)
- x1 et x2 sont les variables explicatives (ici : la surface et le nombre de chambres)
- e est le terme d’erreur, assumé être distribué selon une loi Normale : <math>e_i \rightarrow \mathcal{N}(0,\sigma^2) </math>.
Sous un certain nombre d'hypothèses, la méthode des moindres carrés ordinaires (OLS pour Ordinary Least Square) permet d'obtenir des estimateurs BLUE (Best Linear Unbiased Estimators), c'est-à-dire qui sont sans biais et à variance minimale. Les coefficients estimés sont issus de la minimisation de la somme des carré des résidus entre les valeurs prédites et les valeurs observées,formellement : <math> (\hat{b0} ; \hat{b1}) = \underset{\hat{b0},\hat{b1}}{argmin} \sum_{i=1}^{n} \hat{e_i}^2 = \underset{\hat{b0},\hat{b1}}{argmin} \sum_{i=1}^{n} (y_i - \hat{b0} - \hat{b1} \times x1_i - \hat{b2} \times x2_i) ^2 </math>
Regression linéaire simple
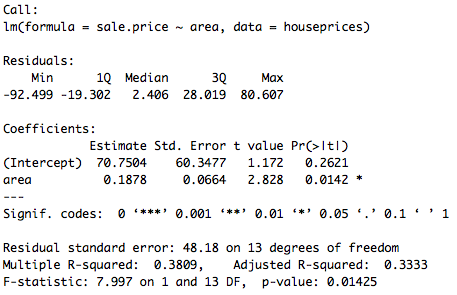
Dans ce cas, on considère une seule variable explicative. Ici, on souhaite donc estimer les coefficients du modèle :<math> sale.price = b0 + b1 \times area + e </math> La commande à utiliser dans R est : lm()
# y = b0 + b1*x1 # Variable à expliquer : y = prix de vente de la maison # Une variable explicative : x1 = Surface au sol de la maison pricereg<-lm(sale.price ~ area, data=houseprices)
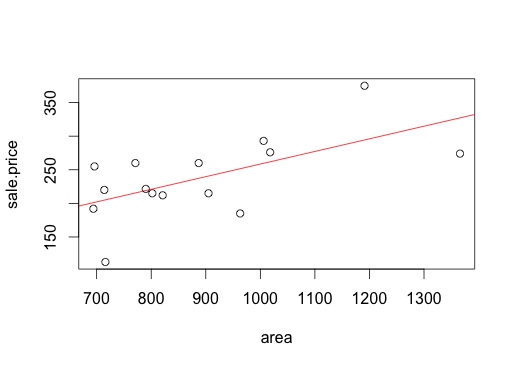
On a donc l'équation de la droite de régression : <math> sale.price= 70.75 + 0.188 \times area + \hat{e} </math> , que l'on peut tracer avec le nuage de points :
# plot : "vraies" valeurs et droite de regression plot(sale.price ~ area, data=houseprices) abline(pricereg, col = "red")
Regression linéaire multiple
Ici, on considère deux (ou plus) variables explicatives. On souhaite donc estimer les coefficients du modèle : <math> sale.price = b0 + b1 \times area + b2 \times bedroom + e </math>
# Variables explicatives : x1 = Surface au sol de la maison, x2 = nombre de chambres pricereg2<-lm(sale.price ~ area + bedrooms , data=houseprices)
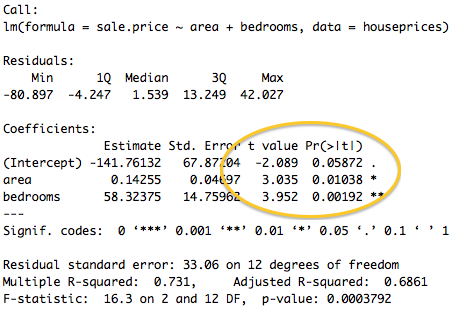
Interprétation
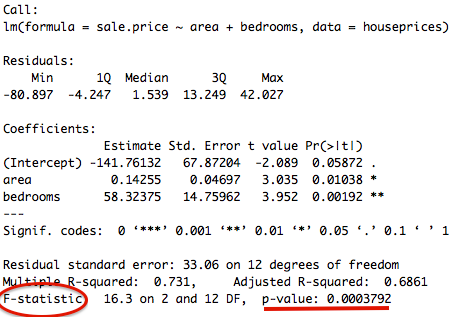
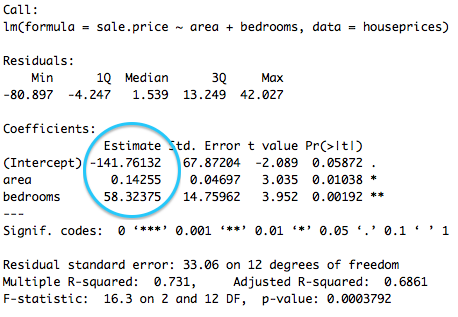
L'équation de la droite de regression est : <math> sale.price = -141.76 + 0.14 \times area + 58.32 \times bedrooms </math>. Les coefficients associés aux variables "area" et "bedrooms" sont significatifs (respectivement à 95% et à 99%, cf : sortie précédente), on peut donc les interpréter. Toutes choses égales par ailleurs, une chambre supplémentaire augmente par exemple le prix de la maison de 58 milles dollars environ, et 100 unités de surface (inconnue) supplémentaires vont l’augmenter de 14 mille dollars, toutes choses égales par ailleurs.
Fonctions (extraction, prédiction,...)
summary
summary() permet de produire les sorties pour chaque regression présentées précédemment. Ainsi, cette fonction affiche : les coefficients estimés, leur écart-type, et la valeur de la statistique t de Student ainsi que la p-value (probabilité que le coefficient soit significativement différent de zéro) associées à chaque coefficient. Sont aussi présentés le R2 et R2 ajusté, ainsi que la statistique F de Fisher (testant la significativité globales des variables), son degré de liberté, et la p-value associée.
#### Regression output summary(pricereg2)
Coefficient
coef() permet de n’extraire que les coefficients estimés.
#### Extraction des coefficients coef(pricereg2)
Confint
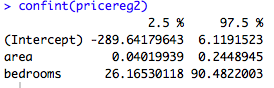
confint() permet d’afficher l’intervalle de confiance à 95% pour les coefficients estimés.
#### Intervalle de confiance (à 95%) des coefficients confint(pricereg2)
Fitted
fitted() permet d’extraire les valeurs prédites.
#### Extraction des valeurs prédites fitted(pricereg2)
Residuals
resid() permet d’extraire les résidus (Valeur prédite - Valeur réelle).
#### Extraction des résidus resid(pricereg2)
Plusieurs hypothèses sous-jacentes au modèle de regression linéaire portent sur les résidus de la regression : indépendance, homoscédasticité (même variance) et normalité. On peut représenter graphiquement les résidus, afin d'observer si ces conditions sont (plus ou moins) respectées. Par exemple, on peut tracer :
- les rédidus en ordonnées
- résidus en ordonnées, valeurs prédites en abcisse.
- résidus en ordonnées, variables explicatives en abcisse.
Si les résidus ne sont pas répartis de manière relativement indépendantes, de part-et d'autre de la droite d'équation y=0 (la moyenne des résidus est nulle pas hypothèse), alors on suspecte un problème (corrélation(s), hétéroscédasticité, ...) que l'on doit corriger avant de pouvoir interpréter un quelconque résultat
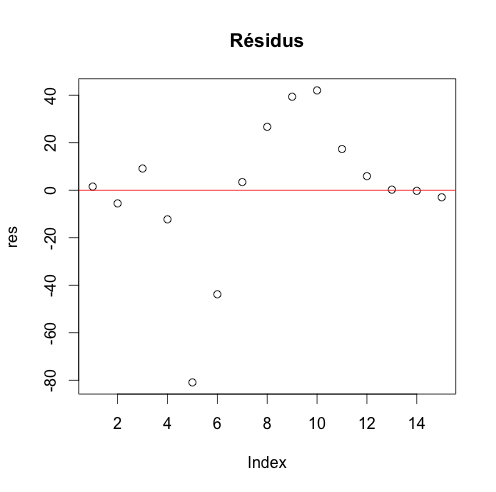
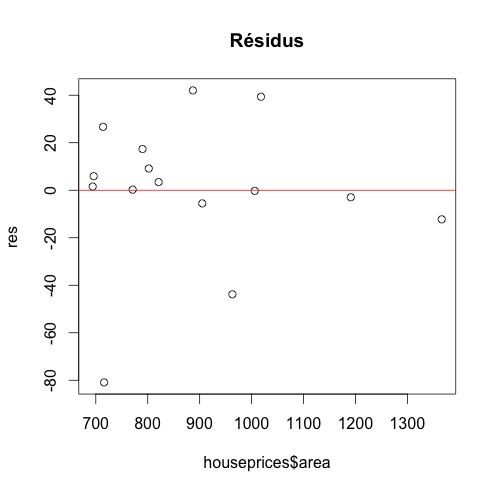
#### résidus res<-resid(pricereg2) plot(res,main="Résidus") abline(h=0,col="red")
On observe que les résidus semblent suivre une tendance. Sur des données en série temporelle (traditionnellement ordonnées chronologiquement), cela pourrait indiquer une auto-corrélation des erreurs (contraire à l'hypothèse d'indépendance), et donc de phénomène non pris-en compte (ex : phénomène de mode, effet saisonnier, etc).
### résidus vs. area plot(houseprices$area,res,main="Résidus") abline(h=0,col="red")
On peut être tenté de voir une diminution des résidus (négatifs) lorsque la surface de la maison augmente (mais ce n'est pas très marqué, d'autant plus que l'on n'a pas beaucoup d'observations).
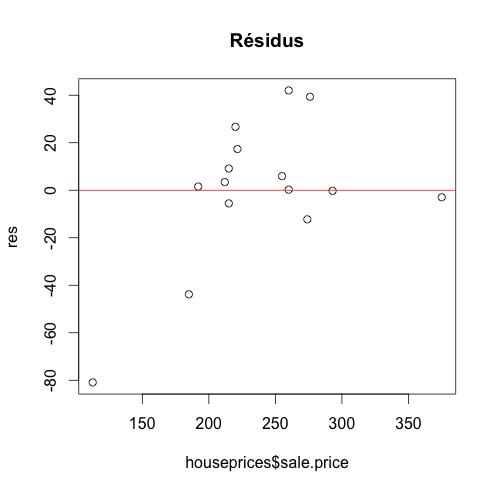
### résidus vs price plot(houseprices$sale.price,res,main="Résidus") abline(h=0,col="red")
Comme sur le graphique précédent, une valeur extrême (petite surface, petit prix) semble perturber un peu l'analyse...
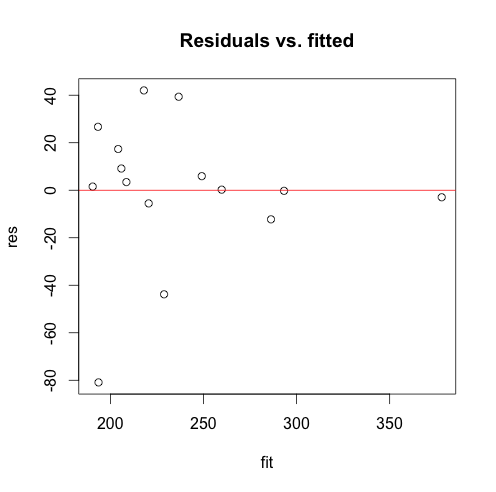
# Extraction des valeurs prédites fit<-fitted(pricereg2) ## residus vs. valeurs prédites plot(fit,res,main="Residuals vs. fitted") abline(h=0,col="red")
Là aussi, on peut être tenté de remarquer une diminution des résidus avec l'augmentation de la valeur prédite, mais ce n'est toutefois toujours pas extrêmement marqué (d'autant plus qu'il n'y a que 15 observations).
Interprétation
Avant d'interpréter les résultats, il convient d'évaluer la significativité du modèle.
Test de significativité globale du modèle
H0 : absence de significativité globale des variables, i.e au moins une variable n'est pas significativement différente de zéro.
Ce test (F-test) est basé sur la statistique de Fisher présentée en bas de la sortie R. Ici, comme la p-value associée est inférieure à 1%, on peut dire que l'on rejète fortement H0, à savoir le modèle est bien globalement significatif. Si cela n'avait pas été le cas, il convient d'exclure une à une chaque variable, afin de déceler le problème.
Interprétation des coefficients
Significativité
Avant d'interpréter un coefficient (sens, magnitude de l'effet), il convient de s'assurer que celui ci est significatif, autrement dit, qu'il est significativement différent de zéro (H0, soit une absence d'effet). Pour cela on utilise un test de Student. On calcule la statistique t pour chaque variable : <math> t_{x}= \frac{coefficient_{x}}{ecart type_{x}} </math>, assumée suivre une loi de Student ; que l'on compare ensuite avec la valeur théorique issue d'une table de Student (déterminée par le niveau du test, et la nombre d'observations).
On utilise souvent un niveau de 5% (soit un intervalle de confiance de 95%). Si la t-value calculée est supérieure (en valeur absolue) à la valeur théorique déterminée, alors on rejète H0 : Le coefficient est bien significativement différent de zéro, et on peut l'interpréter (signe, magnitude,..). Un autre moyen de réaliser le test est de regarder la p-value associée au coefficient, soit la probabilité pour que la valeur t-calculée sit supérieur en valeur absolue à la valeur théorique. Si cette probabilité est inférieur au seuil utilisé (ici 5%), alors le coefficient est significatif.
Ci-dessous, on constate que les deux coefficients sont bien significatifs, on va donc pouvoir les interpréter.
Signe du coefficient
Avec un modèle linéaire, le signe du coefficient associé à une variable indique le sens de l'effet de cette variable sur la variable à expliquer. Par exemple, ici les coefficients de area et bedrooms sont positifs ; cela signifie que toutes choses égales par ailleurs (i.e nombre de chambres constant), augmenter la surface de la maison va avoir tendance à faire augmenter son prix. De même, augmenter le nombre de chambres de la maison, à surface constante va avoir tendance à augmenter son prix.
Magnitude du coefficient
Dans un modèle linéaire basique, on peut interpréter le coefficient associé à la variable x (<math> \beta_{x} </math> comme l'effet de x sur y (variable à expliquer) de la manière suivante : "Toutes choses égales par ailleurs, augmenter x de 1unité (de x) va augmenter/diminuer y de <math> \beta_{x} </math> unités (de y)."
Par exemple ici : Toutes choses égales par ailleurs (i.e nombre de chambres constant), augmenter la surface de la maison de 100 mètres carrés (assumons qu'il s'agit de l'unité de mesure pour la variable surface) va augmenter son prix en moyenne de 14,5 dollars. De même, une chambre supplémentaire, à surface constante, va augmenter le prix de la maison de 58.3 dollars en moyenne.
Cependant, l'interprétation de la magnitude des coefficients va dépendre de la transformation préalable des variables. Notamment, il est courant d'utiliser le logarithme de la variable à expliquer Et/ou de la variable explicative (souvent pour gommer des problèmes d'hétéroscédasticité). On distingue ainsi 4 cas :
- y ~ x : (précédemment) : "Toutes choses égales par ailleurs, augmenter x de 1unité (de x) va augmenter/diminuer y de <math> \beta_{x} </math> unités (de y)."
- y ~ log(x) : "Toutes choses égales par ailleurs, augmenter x de 1 % va augmenter/diminuer y de <math> \beta_{x} </math> unités (de y)." (il s'agit d'une approximation)
- log(y) ~ x : "Toutes choses égales par ailleurs, augmenter x de 1unité (de x) va augmenter/diminuer y de <math> \beta_{x} </math> %." (approximation)
- log(y) ~ log(x) : "Toutes choses égales par ailleurs, augmenter x % va augmenter/diminuer y de <math> \beta_{x} </math> %)." En d'autres termes, <math> \beta_{x} </math> représente l'élasticité de y par rapport à la variable x.
Qualité du modèle
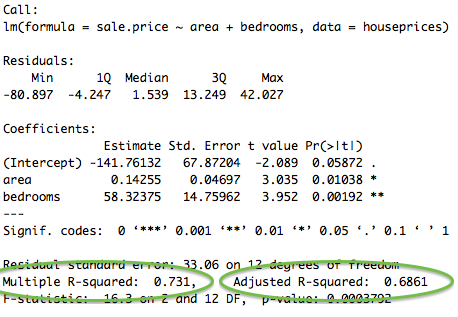
Enfin, on peut regarder la qualité de la régression (au regard des données), mesurée par le coefficient de détermination (R-Squared ou R2), qui se définit comme la part de variation dans la variable y qui est expliquée par des variations dans les variables explicatives (souvent exprimé en %).
Formellement : <math> R^2 = 1 - \frac{SSR}{SST} </math> où SSR représente la somme des carrés des résidus et SST la somme des écarts à la moyenne des valeurs observées.
Plus sa valeur est proche de 1, et plus l'adéquation entre le modèle et les données observées va être forte. Cependant, cette valeur est fortement influencée, entre autres, par le nombre de variables explicatives incluses dans la regression. Le R2 ajusté (Adjusted R-Squared) va alors tenir compte de ce nombre et sera donc plus correct.
Formellement : <math> R^2_{adjusted} = 1 - \frac{SSR/n-k}{SST/n-1} </math>
Ici, il est de 69%, ce qui est plus que correct.
Attention également, même si il n'existe aucune règle, ni aucune échelle précise qui indiquerait pour quelles valeurs du R2, la qualité doit être considérée "mauvaise" ou au contraire comme "excellente", une valeur trop élevée (R2 ou R2 ajusté supérieurs à 85%) peut cacher un grave problème (notamment d'endogénéité), et donc des résultats totalement erronés. De plus, il n'est bien souvent pas possible d'atteindre des valeurs jugées "satisfaisantes", en raison des données à disposition pour l'analyse ; et il n'est donc pas rare que l'économètre doive se contenter d'un R2 de "seulement" 40% par exemple (voire 30%) ! Ici notre 70% est donc plus que convenable, et la recherche d'un R2 élevé ne doit pas être un but en soi..
Predict
La fonction predict() permet de prédire la valeur de y (i.e du prix) pour de nouvelles données (des variables explicatives). Seul les deux premiers arguments sont requis : se.fit permet d’afficher l’écart-type de la valeur prédite, et interval et level permettent afficher ici les valeurs de l’intervalle de confiance fixé à 99%.
#### Prédiction du prix de la maison en fonction de sa superficie et de son nombre de chambres predict(pricereg2, newdata=data.frame(area=800,bedrooms=2), se.fit=TRUE, interval = "prediction", level = 0.99)
Ainsi, le prix estimé d’une maison dont la surface au sol est de 800 unités et qui a 2 chambres serait de 88.92 mille dollars.