Démographie : Différence entre versions
(→Taux de mortalité) |
|||
| (100 révisions intermédiaires par 2 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
= Quelques concepts d'analyse démographique = | = Quelques concepts d'analyse démographique = | ||
| − | Cette page consigne quelques concepts standards pour toute étude démographique. Elle abordera en particulier différentes notions et calculs d'indicateurs classiques que l'on retrouvera dans la plupart des manuels. Dans l'écriture de cette page nous avons plus précisément | + | Cette page consigne quelques concepts standards pour toute étude démographique. Elle abordera en particulier différentes notions et calculs d'indicateurs classiques que l'on retrouvera dans la plupart des manuels. Dans l'écriture de cette page nous avons plus précisément suivi la lecture du manuel de Sid-Ahmed Souiah et Stéphanie Toutain: [http://www.u-cergy.fr/article5992.html L'analyse démographique et spatiale] aux éditions du temps. |
== Structure de la population == | == Structure de la population == | ||
| Ligne 7 : | Ligne 7 : | ||
La densité de population s'exprime en nombre d'habitant au km² ou à l'hectare (ha). Dans la pratique, on peut calculer ceci pour une ville, une agglomération, une région, un pays ou le monde entier. Elle se défini comme le rapport: | La densité de population s'exprime en nombre d'habitant au km² ou à l'hectare (ha). Dans la pratique, on peut calculer ceci pour une ville, une agglomération, une région, un pays ou le monde entier. Elle se défini comme le rapport: | ||
| − | d=P/S | + | '''d=P/S''' |
ou P est la population de la zone et S sa superficie. | ou P est la population de la zone et S sa superficie. | ||
| − | ''Exemple : '' En 2006, dans la région Midi-Pyrénées, on comptait 2 755 000 habitants pour une superficie 45 348 km². La densité pour cette région est donc de 61 hab/km². | + | ''Exemple : '' En 2006, dans la région Midi-Pyrénées, on comptait 2 755 000 habitants pour une superficie de 45 348 km². La densité pour cette région est donc de 61 hab/km². |
| + | |||
| + | d=2 755 000/45 348=61hab/km² | ||
=== Ecart interquartile === | === Ecart interquartile === | ||
L'écart interquartile donne une représentation de la distribution autour de sa médiane. Il est défini dans la même unité que la statistique étudiée et porte sur 50% de la population: | L'écart interquartile donne une représentation de la distribution autour de sa médiane. Il est défini dans la même unité que la statistique étudiée et porte sur 50% de la population: | ||
| − | EIQ=Q<sub>3</sub>-Q<sub>1</sub> | + | '''EIQ=Q<sub>3</sub>-Q<sub>1</sub>''' |
où Q<sub>3</sub> est le troisième quartile et Q<sub>1</sub> le premier. | où Q<sub>3</sub> est le troisième quartile et Q<sub>1</sub> le premier. | ||
| − | ''Exemple :'' Si EIQ=320€, on dit que l'écart de salaire pour 50% de la population, centré autour de la médiane, est de 320€. Pour comparer deux distributions, il est conseillé de | + | ''Exemple :'' Si EIQ=320€, on dit que l'écart de salaire pour 50% de la population, centré autour de la médiane, est de 320€. Pour comparer deux distributions, il est conseillé de mesurer l'écart relatif en divisant l'EIQ par la mediane (Q<sub>2</sub>). |
=== Rapport de masculinité === | === Rapport de masculinité === | ||
Il exprime dans une classe (z) donnée (âge, salaire, géographique,...) le nombre d'hommes pour 100 femmes: | Il exprime dans une classe (z) donnée (âge, salaire, géographique,...) le nombre d'hommes pour 100 femmes: | ||
| − | Rm<sub>z</sub>=(H<sub>z</sub>/F<sub>z</sub>)*100 | + | '''Rm<sub>z</sub>=(H<sub>z</sub>/F<sub>z</sub>)*100''' |
| − | ''Exemple :'' En France, on a environ 105 garçons pour 100 filles à la naissance. | + | ''Exemple :'' En France, on a environ 105 garçons pour 100 filles à la naissance depuis 10 ans. |
| + | |||
| + | Pour 2006 : Rm<sub>z</sub>=(424 930 garçons/405 358 filles)*100=104,83 | ||
=== Rapports de classes d'âges === | === Rapports de classes d'âges === | ||
| Ligne 54 : | Ligne 58 : | ||
Le solde naturel est la différence entre le nombre de naissances vivantes (N) et celui des décés (D) au cours d'une année: | Le solde naturel est la différence entre le nombre de naissances vivantes (N) et celui des décés (D) au cours d'une année: | ||
| − | SN=N-D | + | '''SN=N-D''' |
| − | ''Exemple :'' En | + | ''Exemple :'' En 2006 en France, le nombre de naissances vivantes s'élevait à 830 288 tandis que le nombre de décès atteignait 527 036 personnes. Le solde naturel pour cette année en France est donc de +303 252 habitants. |
| + | |||
| + | SM = 830 288 - 527 036 = 303 252 | ||
=== Taux d'accroissement naturel === | === Taux d'accroissement naturel === | ||
| − | Le taux d'accroissement naturel est la valeur relative du solde naturel, ramené à la population moyenne (P) de la période considérée: | + | Le taux d'accroissement naturel est la valeur relative du solde naturel, ramené à la population moyenne (P) de la période considérée. Ce taux s'exprime habituellement en ‰ (pour mille) et se calcule de la manière suivante : |
| − | TAN=((N-D)/P)*1000 | + | '''TAN=((N-D)/P)*1000=(S/P)*1000''' |
il s'exprime en nombre d'habitants de plus (resp. de moins) si le taux est positif (resp. négatif). | il s'exprime en nombre d'habitants de plus (resp. de moins) si le taux est positif (resp. négatif). | ||
| − | + | ''Exemple :'' La France comptait 63 195 457 habitants en 2006, le taux d'accroissement naturel pour cette année là est de +4,8‰. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | TAN = (303 252/63 195 457)*1000 = +4,8‰ | |
| − | |||
| − | |||
=== Taux de variation d'une population === | === Taux de variation d'une population === | ||
Le taux de variation mesure l'évolution de la population entre deux dates, il se mesure en nombre d'individus pour mille: | Le taux de variation mesure l'évolution de la population entre deux dates, il se mesure en nombre d'individus pour mille: | ||
| − | TV=(PF-PI)/PI | + | '''TV=((PF-PI)/PI)*1000''' |
où, PF est la population en fin de période, et PI celle en début de période. | où, PF est la population en fin de période, et PI celle en début de période. | ||
| + | |||
| + | ''Exemple :'' En 2000, la France comptait 60 750 876 habitants. Entre 2000 et 2006, la population française s'est accrue de 40,24‰ soit de l'ordre de 40 habitants pour mille. | ||
| + | |||
| + | TV = ((63 195 457-60 750 876)/60 750 876)*1000 = 40,24‰ | ||
=== Indice de croissance === | === Indice de croissance === | ||
L'indice de croissance mesure l'évolution de la population par rapport à une année de référence cette fois-ci. Il s'exprime en base cent: | L'indice de croissance mesure l'évolution de la population par rapport à une année de référence cette fois-ci. Il s'exprime en base cent: | ||
| − | IC=Pt/P0*100 | + | |
| + | '''IC=Pt/P0*100''' | ||
où, Pt est la population l'année t donnée et P0 est la population l'année de référence | où, Pt est la population l'année t donnée et P0 est la population l'année de référence | ||
| + | |||
| + | ''Exemple :'' Indices de croissance de la population de la France métropolitaine à différents recensements (base 100 en 1968) | ||
| + | |||
| + | [[Image:tableau.jpg]] | ||
| + | |||
| + | IC<sub>1968-1999</sub> = (58 253 551/49 444 772)*100 = 118 | ||
=== Taux moyen d'accroissement annuel=== | === Taux moyen d'accroissement annuel=== | ||
En observant l'évolution entre la population initiale (PI) et finale (PF) au cours d'une période de N années, on peut calculer le taux moyen d'accroissement annuel: | En observant l'évolution entre la population initiale (PI) et finale (PF) au cours d'une période de N années, on peut calculer le taux moyen d'accroissement annuel: | ||
| − | r=[(PF/PI)<sup>1/N</sup>-1]* | + | '''r=[(PF/PI)<sup>1/N</sup>-1]*1000''' |
Si r est positif on en déduit que la population s'est accrue chaque année en moyenne de r habitants pour mille. | Si r est positif on en déduit que la population s'est accrue chaque année en moyenne de r habitants pour mille. | ||
| + | |||
| + | ''Exemple :'' Entre 2000 et 2006, la population française s'est accrue, en moyenne, chaque année de 6,6‰ soit un peu moins de 7 habitants pour mille. | ||
| + | |||
| + | r= ((63 195 457 / 60 750 876)<sup>1/6</sup>-1]*1000 = 6,6‰ | ||
=== Temps de doublement === | === Temps de doublement === | ||
Lorsqu'on connait le taux moyen d'accroissement annuel (r) on peut calculer le nombre d'année qu'il faudrait à une zone pour que sa population double: | Lorsqu'on connait le taux moyen d'accroissement annuel (r) on peut calculer le nombre d'année qu'il faudrait à une zone pour que sa population double: | ||
| − | N=log(2)/log(1+r) | + | '''N=log(2)/log(1+r)''' |
| + | |||
| + | ''Exemple :'' Sachant que le taux moyen d'accroissement annuel de la population française entre 2000 et 2006 est estimé à 6,6‰ et si ce taux restait constant à l'avenir, la population française doublerait théoriquement dans 105 ans soit en 2111. | ||
| + | |||
| + | N= log(2)/log(1+0,0066) = 105 | ||
ou triple: | ou triple: | ||
| − | N=log(3)/log(1+r) | + | '''N=log(3)/log(1+r)''' |
| + | |||
| + | ''Exemple :'' Avec les mêmes hypothèses que précedemment, cette population triplerait dans 167 ans soit en 2173. | ||
| + | |||
| + | N= log(3)/log(1+0,0066) = 167 | ||
=== Taux de renouvellement global === | === Taux de renouvellement global === | ||
Lorsqu'on connait le nombre de naissances (N) de décés (D) d'immigrés (I) et d'émigrés (E) on peut calculer le taux de renouvellement d'une population dû à ces facteurs démographiques, c'est à dire la proportion de la population qui a subi un évènement démographique : | Lorsqu'on connait le nombre de naissances (N) de décés (D) d'immigrés (I) et d'émigrés (E) on peut calculer le taux de renouvellement d'une population dû à ces facteurs démographiques, c'est à dire la proportion de la population qui a subi un évènement démographique : | ||
| − | TRG=[(N+D+I+E)/P]*100 | + | '''TRG=[(N+D+I+E)/P]*100''' |
où, P est la population moyenne sur la période. On peut décomposer ce taux en distinguant la part qui est due à une entré de population et celle qui est due à une sortie: | où, P est la population moyenne sur la période. On peut décomposer ce taux en distinguant la part qui est due à une entré de population et celle qui est due à une sortie: | ||
| − | TRG=[(N+I)/P]*100 + [(D+E)/P]*100 | + | '''TRG=[(N+I)/P]*100 + [(D+E)/P]*100''' |
| + | |||
| + | ''Exemple : '' | ||
| + | |||
| + | En 1990 en France métropolitaine, un peu plus de 4% de la population a subi un évènement démographique majeur soit par des prélèvements (mortalité ou émigration), soit par des apports (natalité ou immigration). | ||
| + | |||
| + | P=56 401 920, N=658 105, D=471 866, I=682 613, E=549 689. | ||
| + | |||
| + | TRG = ((658 105 + 682 613)/56 401 920)*100 + ((471 866 + 549 689)/56 401 920)*100 = 4,19% | ||
== Flux migratoire == | == Flux migratoire == | ||
| Ligne 121 : | Ligne 148 : | ||
C'est la différence en valeur entre le nombre d'immigrants (I) et celui d'émigrants (E): | C'est la différence en valeur entre le nombre d'immigrants (I) et celui d'émigrants (E): | ||
| − | SM=I-E | + | '''SM=I-E''' |
| + | |||
| + | ''Exemple :'' En 1990, la population française s'est accrue de 132 924 habitants. | ||
| + | |||
| + | SM = 682 613 - 549 689 = 132 924 habitants | ||
=== Taux d'immigration === | === Taux d'immigration === | ||
C'est le rapport entre les immigrations (I) et la population moyenne (P): | C'est le rapport entre les immigrations (I) et la population moyenne (P): | ||
| − | TI=(I/P)*100 | + | '''TI=(I/P)*100''' |
| + | |||
| + | ''Exemple :'' Le taux d'immigration en 1990 atteignait 1,21%. | ||
| + | |||
| + | TI = (682 613/56 401 920)*100 = 1,21% | ||
=== Taux d'émigration === | === Taux d'émigration === | ||
C'est le rapport entre les émigrations (E) et la population moyenne (P): | C'est le rapport entre les émigrations (E) et la population moyenne (P): | ||
| − | TE=(E/P)*100 | + | '''TE=(E/P)*100''' |
| + | |||
| + | ''Exemple :'' Le taux d'émigration s'élevait à 0,97% en 1990. | ||
| + | |||
| + | TE = (549 689/56 401 920)*100 = 0,97% | ||
=== Taux de migration nette === | === Taux de migration nette === | ||
| − | C'est la différence des deux taux précédents | + | C'est la différence des deux taux précédents. |
| − | TMN=TI-TE | + | '''TMN=TI-TE''' |
| + | |||
| + | ''Exemple :'' En 1990, le taux de migration nette était de +0,24%. | ||
| + | |||
| + | TMN = 1,21 - 0,97 = +0,24% | ||
| + | |||
| + | === Taux de migration total === | ||
| + | C'est la somme des taux d'immigration et d'émigration sur une année. | ||
| + | |||
| + | '''TMT=TI+TE''' | ||
| + | |||
| + | ''Exemple :'' En 1990, le taux de migration total était de 2,18%. | ||
| + | |||
| + | TMT = 1,21 + 0,97 = 2,18% | ||
=== Taux d'accroissement migratoire === | === Taux d'accroissement migratoire === | ||
Il rapporte le solde migratoire (SM) à la population moyenne (P) une année donnée et peut être positif (flux d'entrée) ou négatif (flux de sorties): | Il rapporte le solde migratoire (SM) à la population moyenne (P) une année donnée et peut être positif (flux d'entrée) ou négatif (flux de sorties): | ||
| − | TAM=(SM/P)*100 | + | '''TAM=(SM/P)*100''' |
| + | |||
| + | ''Exemple :'' En 1990, le taux d'accroissement migratoire était de +0,24%. | ||
| + | |||
| + | TAM = (132 924 / 56 401 920)*100 = +0,24% | ||
| + | |||
| + | |||
| + | [[Category:Portail:Langage-commun]] | ||
| + | [[Category: Economie-social]] | ||
Version actuelle datée du 24 août 2017 à 10:02
Sommaire
Quelques concepts d'analyse démographique
Cette page consigne quelques concepts standards pour toute étude démographique. Elle abordera en particulier différentes notions et calculs d'indicateurs classiques que l'on retrouvera dans la plupart des manuels. Dans l'écriture de cette page nous avons plus précisément suivi la lecture du manuel de Sid-Ahmed Souiah et Stéphanie Toutain: L'analyse démographique et spatiale aux éditions du temps.
Structure de la population
Densité de population
La densité de population s'exprime en nombre d'habitant au km² ou à l'hectare (ha). Dans la pratique, on peut calculer ceci pour une ville, une agglomération, une région, un pays ou le monde entier. Elle se défini comme le rapport:
d=P/S
ou P est la population de la zone et S sa superficie.
Exemple : En 2006, dans la région Midi-Pyrénées, on comptait 2 755 000 habitants pour une superficie de 45 348 km². La densité pour cette région est donc de 61 hab/km².
d=2 755 000/45 348=61hab/km²
Ecart interquartile
L'écart interquartile donne une représentation de la distribution autour de sa médiane. Il est défini dans la même unité que la statistique étudiée et porte sur 50% de la population:
EIQ=Q3-Q1
où Q3 est le troisième quartile et Q1 le premier.
Exemple : Si EIQ=320€, on dit que l'écart de salaire pour 50% de la population, centré autour de la médiane, est de 320€. Pour comparer deux distributions, il est conseillé de mesurer l'écart relatif en divisant l'EIQ par la mediane (Q2).
Rapport de masculinité
Il exprime dans une classe (z) donnée (âge, salaire, géographique,...) le nombre d'hommes pour 100 femmes:
Rmz=(Hz/Fz)*100
Exemple : En France, on a environ 105 garçons pour 100 filles à la naissance depuis 10 ans.
Pour 2006 : Rmz=(424 930 garçons/405 358 filles)*100=104,83
Rapports de classes d'âges
Le rapport de jeunesse, donne le nombre de jeunes de moins de 20 ans (N(0-19ans)) pour 100 personnes d'âges actifs:
Rj=(N(0-19ans)/N(20-60ans))*100
Le rapport de dépendance, prend en plus en compte les plus de 60 ans:
Rd=[(N(0-19ans)+N(60ans et plus))/N(20-60ans)]*100
Le rapport de vieillesse, quand à lui, donne le nombre de personnes de 60 ans et plus pour 100 personnes actives:
Rv=(N(60ans et plus)/N(20-60ans))*100
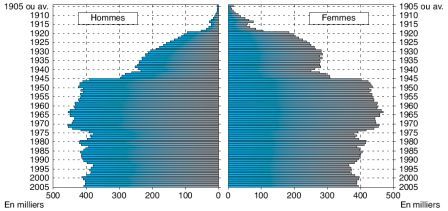
Pyramide des âges
La pyramide des âges représente la répartition d'une population par tranche d'âge et par sexe à un instant donné, pour une population donnée. Elle peut décrire la population d'une région ou d'un pays, ou une sous-population (les agriculteurs ou les médecins par exemple).
Exemple : Pyramide des âges en France.
Evolution de la population
Solde naturel
Le solde naturel est la différence entre le nombre de naissances vivantes (N) et celui des décés (D) au cours d'une année:
SN=N-D
Exemple : En 2006 en France, le nombre de naissances vivantes s'élevait à 830 288 tandis que le nombre de décès atteignait 527 036 personnes. Le solde naturel pour cette année en France est donc de +303 252 habitants.
SM = 830 288 - 527 036 = 303 252
Taux d'accroissement naturel
Le taux d'accroissement naturel est la valeur relative du solde naturel, ramené à la population moyenne (P) de la période considérée. Ce taux s'exprime habituellement en ‰ (pour mille) et se calcule de la manière suivante :
TAN=((N-D)/P)*1000=(S/P)*1000
il s'exprime en nombre d'habitants de plus (resp. de moins) si le taux est positif (resp. négatif).
Exemple : La France comptait 63 195 457 habitants en 2006, le taux d'accroissement naturel pour cette année là est de +4,8‰.
TAN = (303 252/63 195 457)*1000 = +4,8‰
Taux de variation d'une population
Le taux de variation mesure l'évolution de la population entre deux dates, il se mesure en nombre d'individus pour mille:
TV=((PF-PI)/PI)*1000
où, PF est la population en fin de période, et PI celle en début de période.
Exemple : En 2000, la France comptait 60 750 876 habitants. Entre 2000 et 2006, la population française s'est accrue de 40,24‰ soit de l'ordre de 40 habitants pour mille.
TV = ((63 195 457-60 750 876)/60 750 876)*1000 = 40,24‰
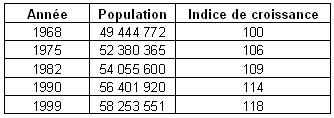
Indice de croissance
L'indice de croissance mesure l'évolution de la population par rapport à une année de référence cette fois-ci. Il s'exprime en base cent:
IC=Pt/P0*100
où, Pt est la population l'année t donnée et P0 est la population l'année de référence
Exemple : Indices de croissance de la population de la France métropolitaine à différents recensements (base 100 en 1968)
IC1968-1999 = (58 253 551/49 444 772)*100 = 118
Taux moyen d'accroissement annuel
En observant l'évolution entre la population initiale (PI) et finale (PF) au cours d'une période de N années, on peut calculer le taux moyen d'accroissement annuel:
r=[(PF/PI)1/N-1]*1000
Si r est positif on en déduit que la population s'est accrue chaque année en moyenne de r habitants pour mille.
Exemple : Entre 2000 et 2006, la population française s'est accrue, en moyenne, chaque année de 6,6‰ soit un peu moins de 7 habitants pour mille.
r= ((63 195 457 / 60 750 876)1/6-1]*1000 = 6,6‰
Temps de doublement
Lorsqu'on connait le taux moyen d'accroissement annuel (r) on peut calculer le nombre d'année qu'il faudrait à une zone pour que sa population double:
N=log(2)/log(1+r)
Exemple : Sachant que le taux moyen d'accroissement annuel de la population française entre 2000 et 2006 est estimé à 6,6‰ et si ce taux restait constant à l'avenir, la population française doublerait théoriquement dans 105 ans soit en 2111.
N= log(2)/log(1+0,0066) = 105
ou triple:
N=log(3)/log(1+r)
Exemple : Avec les mêmes hypothèses que précedemment, cette population triplerait dans 167 ans soit en 2173.
N= log(3)/log(1+0,0066) = 167
Taux de renouvellement global
Lorsqu'on connait le nombre de naissances (N) de décés (D) d'immigrés (I) et d'émigrés (E) on peut calculer le taux de renouvellement d'une population dû à ces facteurs démographiques, c'est à dire la proportion de la population qui a subi un évènement démographique :
TRG=[(N+D+I+E)/P]*100
où, P est la population moyenne sur la période. On peut décomposer ce taux en distinguant la part qui est due à une entré de population et celle qui est due à une sortie:
TRG=[(N+I)/P]*100 + [(D+E)/P]*100
Exemple :
En 1990 en France métropolitaine, un peu plus de 4% de la population a subi un évènement démographique majeur soit par des prélèvements (mortalité ou émigration), soit par des apports (natalité ou immigration).
P=56 401 920, N=658 105, D=471 866, I=682 613, E=549 689.
TRG = ((658 105 + 682 613)/56 401 920)*100 + ((471 866 + 549 689)/56 401 920)*100 = 4,19%
Flux migratoire
Solde migratoire
C'est la différence en valeur entre le nombre d'immigrants (I) et celui d'émigrants (E):
SM=I-E
Exemple : En 1990, la population française s'est accrue de 132 924 habitants.
SM = 682 613 - 549 689 = 132 924 habitants
Taux d'immigration
C'est le rapport entre les immigrations (I) et la population moyenne (P):
TI=(I/P)*100
Exemple : Le taux d'immigration en 1990 atteignait 1,21%.
TI = (682 613/56 401 920)*100 = 1,21%
Taux d'émigration
C'est le rapport entre les émigrations (E) et la population moyenne (P):
TE=(E/P)*100
Exemple : Le taux d'émigration s'élevait à 0,97% en 1990.
TE = (549 689/56 401 920)*100 = 0,97%
Taux de migration nette
C'est la différence des deux taux précédents.
TMN=TI-TE
Exemple : En 1990, le taux de migration nette était de +0,24%.
TMN = 1,21 - 0,97 = +0,24%
Taux de migration total
C'est la somme des taux d'immigration et d'émigration sur une année.
TMT=TI+TE
Exemple : En 1990, le taux de migration total était de 2,18%.
TMT = 1,21 + 0,97 = 2,18%
Taux d'accroissement migratoire
Il rapporte le solde migratoire (SM) à la population moyenne (P) une année donnée et peut être positif (flux d'entrée) ou négatif (flux de sorties):
TAM=(SM/P)*100
Exemple : En 1990, le taux d'accroissement migratoire était de +0,24%.
TAM = (132 924 / 56 401 920)*100 = +0,24%