Statistiques descriptives avec R : Différence entre versions

De Wiki ODR
Aller à : navigation, rechercher
(Page créée avec « == Données == Pour illustrer, on utilise le jeu de données « iris » de R, qui contient 150 observations de 5 variables : * Sepal.Length : longueur de la sépale * ... »)
 
 
(7 révisions intermédiaires par un autre utilisateur non affichées)
Ligne 1 : Ligne 1 :
  
 
== Données ==  
 
== Données ==  
−
Pour illustrer, on utilise le jeu de données « iris » de R, qui contient 150 observations de 5 variables :
+
Pour illustrer, on utilise le jeu de données « iris » de R.
 +
<pre>
 +
###### charger les données
 +
data(iris)
 +
</pre>
 +
 
 +
Il contient 150 observations de 5 variables :
 
* Sepal.Length : longueur de la sépale
 
* Sepal.Length : longueur de la sépale
 
*  Sepal.Width : largeur de la sépale  
 
*  Sepal.Width : largeur de la sépale  
Ligne 46 : Ligne 52 :
 
==== Statistiques ====
 
==== Statistiques ====
 
Pour chaque variable, il est aussi possible d’obtenir séparément les statistiques suivantes (x est une variable quantitative)
 
Pour chaque variable, il est aussi possible d’obtenir séparément les statistiques suivantes (x est une variable quantitative)
−
sum(x)      # pour la somme
 
−
• mean(x)    # pour la moyenne
 
−
• var(x)      # pour la variance
 
−
• sd(x)      # pour l'écart type
 
−
• min(x)      # pour le minimum
 
−
• max(x)      # pour le maximum
 
−
• median(x)  # pour la médiane
 
−
• quantile(x) # pour les quantiles à 0, 25%,50%,75% et 100%
 
−
• length(x)  # pour le nombre d’observations pour la variable
 
  
 +
{| class="wikitable" border="1"
 +
|-
 +
! Fonction
 +
! Opération
 +
|-
 +
| sum(x)
 +
| somme
 +
|-
 +
| mean(x)
 +
| moyenne
 +
|-
 +
| var(x)
 +
| variance
 +
|-
 +
| sd(x)
 +
| écart-type
 +
|-
 +
| min(x)
 +
| minimum
 +
|-
 +
| max(x)
 +
| maximum
 +
|-
 +
| median(x)
 +
| médiane
 +
|-
 +
| quantile(x)
 +
| quantiles à 0, 25%,50%,75% et 100%
 +
|-
 +
| length(x)
 +
| Nombre d'observations pour la variable
 +
|}
  
 
==== Représentation graphique ====  
 
==== Représentation graphique ====  
 
Pour les variables quantitatives, le boxplot est souvent utilisé pour résumer de manière graphique des statistiques descriptives sur chaque variable.  
 
Pour les variables quantitatives, le boxplot est souvent utilisé pour résumer de manière graphique des statistiques descriptives sur chaque variable.  
 +
 +
<pre>
 +
#boxplot
 +
boxplot(iris$Sepal.Length, col = c("yellow"),main = "Boxplot", ylab = "Quantiles")
 +
</pre>
 +
 +
[[Fichier:boxplot_irislength.png]]
  
 
Ci dessous, on sélectionne toutes les variables quantitatives. Le logiciel présentera les boxplots côte-à-côte.  
 
Ci dessous, on sélectionne toutes les variables quantitatives. Le logiciel présentera les boxplots côte-à-côte.  
Ligne 134 : Ligne 170 :
 
prop.table(table_Species)
 
prop.table(table_Species)
 
</pre>
 
</pre>
 +
 +
[[Fichier:proponevar_iris.png]]
  
 
==== Représentation graphique ====  
 
==== Représentation graphique ====  
Ligne 144 : Ligne 182 :
 
         xlab="Nombre d'iris",
 
         xlab="Nombre d'iris",
 
         col="orange")
 
         col="orange")
−
margin.table(table_Species)
 
 
</pre>
 
</pre>
  
Ligne 158 : Ligne 195 :
 
==== Statistiques ====
 
==== Statistiques ====
  
−
Un moyen d’évaluer l'intensité de la liaison entre deux variables est de calculer le coefficient de corrélation (linéaire) :<br />
+
Un moyen d’évaluer l'intensité de la liaison entre deux variables est de calculer le coefficient de corrélation (linéaire) ou coefficient de corrélation de pearson.<br />
  
 
<math> rho(X,Y)=\frac{cov(X,Y)}{sigmaX \times sigmaY} </math>
 
<math> rho(X,Y)=\frac{cov(X,Y)}{sigmaX \times sigmaY} </math>
Ligne 171 : Ligne 208 :
 
[[Fichier:coeffcorr_iris.png]]
 
[[Fichier:coeffcorr_iris.png]]
  
−
Le test peut aussi être directement effectué par la fonction cor.test(X,Y,method=« method").
+
Le test de corrélation peut aussi être directement effectué par la fonction cor.test(X,Y,method=« method").
  
 +
'''<big>H0 : corrélation entre les variables</big>
 +
'''
 
<pre>
 
<pre>
 
## test
 
## test
Ligne 179 : Ligne 218 :
  
 
[[Fichier:testcorr_iris.png]]
 
[[Fichier:testcorr_iris.png]]
 +
 +
Ici, on ne parvient pas à rejeter H0 (p-value>15%), i.e les deux variables sont effectivement corrélées.
  
 
==== Représentation graphique ====
 
==== Représentation graphique ====
Ligne 194 : Ligne 235 :
 
=== Une quantitative, une qualitative ===
 
=== Une quantitative, une qualitative ===
  
−
On étudie les caractéristiques de la variable quantitative (notée X), sur les sous-populations définies par les modalités de la variable qualitative (notée Y).
+
On étudie les caractéristiques de la variable quantitative (notée X), sur les sous-populations définies par les modalités de la variable qualitative (notée Y). <br />
  
−
Le package « psych » permet de calculer des statistiques de base par groupe (les groupes étant définis par les modalités d’une variable). Les statistiques présentées sont celles calculées par la fonction describe() (contenue par défaut dans R), et ne sont pertinentes que pour des variables quantitatives.  
+
==== Statistiques ====
−
Elles sont (dans l’ordre) : Le nombre d’observations, la moyenne, l’écart-type, la médiane, la moyenne tronquée (calculée en enlevant les 5 plus petites et 5 plus grandes valeurs), la déviation absolue à la médiane, le minimum, le maximum, l’étendue (minimum-maximum), le coefficient d’assiymétrie (skew), la Kurtosis et le standard error.  
+
La fonction suivante permet de calculer des statistiques de base (fonction summary) par groupe (les groupes étant définis par les modalités d’une variable).
 +
Par exemple, ici des statistiques pour les iris de chaque espèce, séparément.
 +
 
 +
<pre>
 +
###### descriptive statistics by group
 +
by(iris[,1:4], INDICES=iris[,"Species"], FUN=summary)
 +
</pre>
 +
 
 +
[[Fichier:by_iris.png]]
 +
 
 +
Le package « psych » permet de calculer les statistiques présentées par la fonction describe() (contenue par défaut dans R).  
 +
Elles sont (dans l’ordre) :  
 +
* Le nombre d’observations
 +
* la moyenne
 +
* l’écart-type  
 +
* la médiane  
 +
* la moyenne tronquée (calculée en enlevant les 5 plus petites et 5 plus grandes valeurs)  
 +
*  la déviation absolue à la médiane  
 +
*  le minimum  
 +
*  le maximum  
 +
*  l’étendue (minimum-maximum)  
 +
*  le coefficient d’assiymétrie (skew)  
 +
*  la Kurtosis  
 +
* le standard error.  
  
−
Par exemple, ici des statistiques pour les iris de chaque espèce, séparément.
 
 
<pre>
 
<pre>
 
## Package psych
 
## Package psych
Ligne 236 : Ligne 299 :
  
 
[[Fichier:boxplotparralleles_iris.png]]
 
[[Fichier:boxplotparralleles_iris.png]]
 +
 +
==== Test====
 +
 +
On peut vouloir tester si la longueur des pétales des iris de l'espèce "setosa" est significativement différente (au sens statistique du terme) de celle des pétales de l'espèce "versicolor". Pour celà, on effectue un test de Student.
 +
 +
'''<big>H0 : Différence non significative (i.e nulle)
 +
</big>'''
 +
<pre>
 +
#Test de Student
 +
t.test(iris_versicolor$Petal.Length,iris_setosa$Petal.Length)
 +
</pre>
 +
 +
[[Fichier:ttest_iris.png]]
 +
 +
La p-value étant quasiment nulle, on rejète fortement H0. Cela signifie qu'il existe bien une différence significative entre la taille des pétales d'iris de ces deux espèces.
 +
 +
De manière plus générale, on peut vouloir tester si la longueur des pétales des Iris diffère de manière significative entre les fleurs de différentes espèces (pour les trois espèces représentées dans la base de données). Pour cela, on réalise une ANOVA.
 +
 +
<big>'''H0 : Différence non significative
 +
'''</big>
 +
<pre>
 +
# ANOVA
 +
anova <- aov(Petal.Length ~ Species, data=iris)
 +
anova
 +
summary(anova)
 +
</pre>
 +
 +
[[Fichier:anova.png]]
 +
 +
La p-value étant quasiment nulle, on rejète fortement H0. Cela signifie qu'il existe bien une différence significative entre la taille des pétales d'iris de deux espèces différentes (parmi les trois espèces des données).
  
 
=== Deux variables qualitatives : ===  
 
=== Deux variables qualitatives : ===  
 +
 +
La base de données utilisée ne contenant qu'une seule variable qualitative, on en crée une seconde, afin de pouvoir illustrer la suite par des exemples. Fictive, cette variable est basée sur la variable Sepal.Length et prend au choix la valeur « petite » (Sepal.Length<=5), « moyenne » (Sepal.Length>5 mais <=6) ou « grande »(Sepal.Length>6), pour chaque observation.
 +
<pre>
 +
## On crée une nouvelle variable facteur :
 +
iris$Sepal.Length_cat[iris$Sepal.Length<=5]<-"petit"
 +
iris$Sepal.Length_cat[iris$Sepal.Length<=6 & iris$Sepal.Length>5]<-"moyen"
 +
iris$Sepal.Length_cat[iris$Sepal.Length>6]<-"grand"
 +
</pre>
  
 
==== Tableau ====
 
==== Tableau ====
Ligne 243 : Ligne 344 :
 
On peut résumer ici les effectifs sous la forme d’un tableau à double entrée, toujours avec la fonction table, avec la syntaxe suivante : table(variable1,variable2,……variablen). A noter que le nombre de variables n’est pas limité à deux.
 
On peut résumer ici les effectifs sous la forme d’un tableau à double entrée, toujours avec la fonction table, avec la syntaxe suivante : table(variable1,variable2,……variablen). A noter que le nombre de variables n’est pas limité à deux.
  
−
Pour illustrer, on crée une seconde variable qualitative car il n’y en a qu’une dans notre base de donnée. Fictive, cette variable est basée sur la variable Sepal.Length et prend au choix la valeur « petite », « moyenne » ou « grande », pour chaque observation.
 
 
<pre>
 
<pre>
 
## Table
 
## Table
Ligne 306 : Ligne 406 :
 
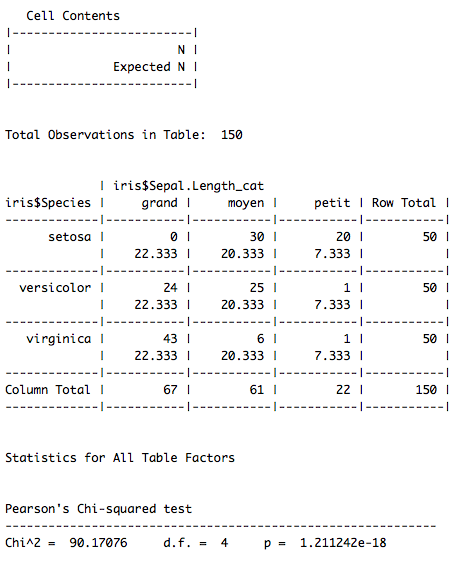
CrossTable(iris$Species,iris$Sepal.Length_cat,prop.t=FALSE,prop.c=FALSE,prop.r=FALSE,prop.chisq=TRUE,chisq=TRUE,expected=TRUE)
 
CrossTable(iris$Species,iris$Sepal.Length_cat,prop.t=FALSE,prop.c=FALSE,prop.r=FALSE,prop.chisq=TRUE,chisq=TRUE,expected=TRUE)
 
</pre>
 
</pre>
 +
 +
[[Fichier:tablekhi_iris.png]]
 +
 +
 +
 +
[[Category:Aides statistiques]]

Version actuelle datée du 7 septembre 2017 à 13:33

Données

Pour illustrer, on utilise le jeu de données « iris » de R. 

###### charger les données
data(iris)

Il contient 150 observations de 5 variables :

  • Sepal.Length : longueur de la sépale
  • Sepal.Width : largeur de la sépale
  • Petal.Length : longueur du pétale
  • Petal.Width : largeur du pétale
  • Species : espèce de la fleur.

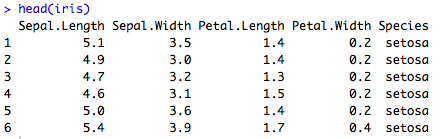
La fonction head(dataset) permet d’avoir un aperçu des premières lignes du jeu de données : 

head(iris)

Headiris.png

On a ainsi : 4 variables de type quantitatif, et une de type qualitatif (Species).

Statistiques univariées

Aperçu global

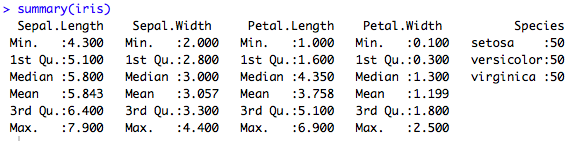
La fonction summary(dataset) permet de visualiser des statistiques de base pour chaque variable : Pour les variables quantitatives : Minimum, maximum, moyenne, médiane, 1er quartile, 3ème quartile. Pour les variables qualitatives : Nombre d’observations par classe. 

summary(iris)

Summary iris.png

Différents packages permettent aussi d’obtenir des statistiques sur une base de données. Par exemple, la fonction describe() du package Hmisc permet d’obtenir pour chaque variable : le nombre d’observations, le nombre de valeurs manquantes, la moyenne, les quantiles à 5, 10,25,50,75,90, et 95%, les 5 plus basses valeurs, et 5 plus hautes.

Pour les variables qualitatives, describe() donne le nombre d’observations, le nombre de valeurs manquantes, et le nombre de niveaux pour la variable ; ainsi que le nombre d’observations pour chaque niveau de la variable (et la proportion).

Attention à bien charger le package Hmisc avant d’exécuter la fonction, sinon la fonction describe() par défaut sera appliquée, produisant des statistiques pertinentes pour des variables quantitatives, mais non pour des variables qualitatives. 

 library(Hmisc)
describe(iris)

Describe iris.png

Les fonctions présentées peuvent aussi être utilisées sur une variable en particulier seulement, et non pas sur l’ensemble des variables composant la base de données.

Variables quantitatives

Statistiques

Pour chaque variable, il est aussi possible d’obtenir séparément les statistiques suivantes (x est une variable quantitative)

Fonction Opération
sum(x) somme
mean(x) moyenne
var(x) variance
sd(x) écart-type
min(x) minimum
max(x) maximum
median(x) médiane
quantile(x) quantiles à 0, 25%,50%,75% et 100%
length(x) Nombre d'observations pour la variable

Représentation graphique

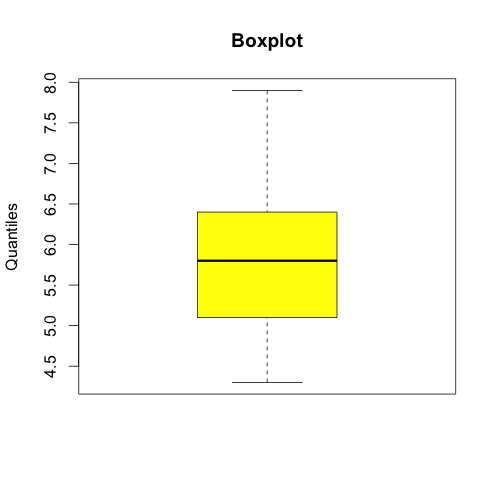
Pour les variables quantitatives, le boxplot est souvent utilisé pour résumer de manière graphique des statistiques descriptives sur chaque variable. 

#boxplot 
boxplot(iris$Sepal.Length, col = c("yellow"),main = "Boxplot", ylab = "Quantiles")

Boxplot irislength.png

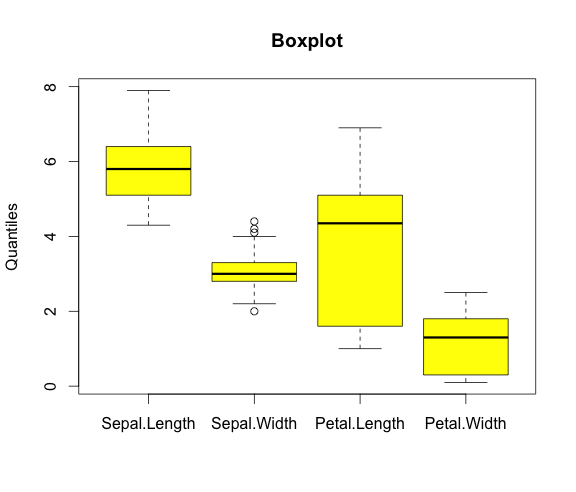
Ci dessous, on sélectionne toutes les variables quantitatives. Le logiciel présentera les boxplots côte-à-côte. 

#boxplot 
boxplot(iris[,c('Sepal.Length','Sepal.Width','Petal.Length','Petal.Width')],
        col = c("yellow"),                 #Pour la couleur
        main = paste("Boxplot"),     #Pour le titre
        ylab = "Quantiles")              #Pour le titre de l’axe des ordonnées

Boxplot iris.png

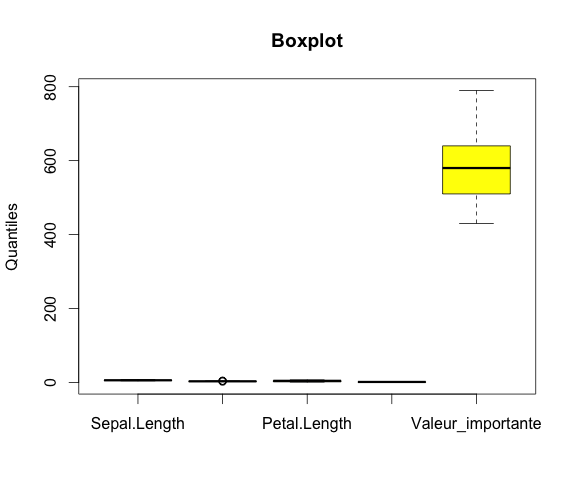
A noter que cela peut produire un graphique peut lisible en cas de trop grandes différences d’unités. Par exemple ici, on crée une variable fictive en multipliant la variable Sepal.Length par 100. 

## Avec une grande différence d'unités
iris$Valeur_importante<-iris$Sepal.Length*100
 
boxplot(iris[,c('Sepal.Length','Sepal.Width','Petal.Length','Petal.Width','Valeur_importante')],
        col = c("yellow"),
        main = paste("Boxplot"),
        ylab = "Quantiles")

Boxplot iris tpgd.png


Il peut donc être préférable d’effectuer le boxplot pour une seule variable à la fois. 

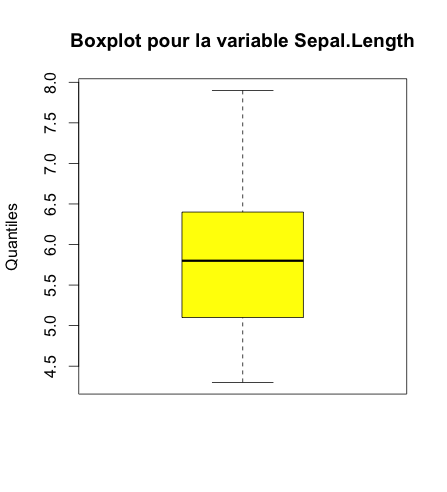
## Pour une seule variable
boxplot(iris$Sepal.Length, 
        col = c("yellow"),
        main = paste("Boxplot pour la variable Sepal.Length"),
        ylab = "Quantiles")

Boxplot unevar.png


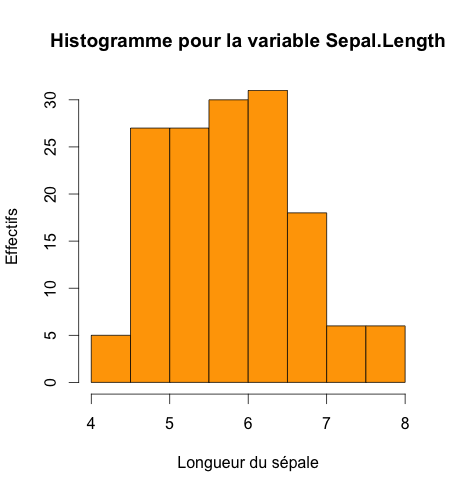
Il est aussi courant de tracer un histogramme des valeurs pour la variable. (Attention, à ne pas confondre avec le diagramme en bâtons (ou barplots), réservé aux variables qualitatives !!!!!!) 

## HISTOGRAMME
hist(iris$Sepal.Length, 
      col = c("orange"),
      main = paste("Histogramme pour la variable Sepal.Length"),
      ylab = "Effectifs",
      xlab = "Longueur du sépale")

Histogramme iris.png


Variables qualitatives

Statistiques

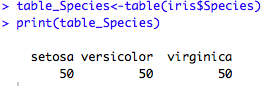
Pour un résumé pertinent d’une variable qualitative, on trace un tableau des effectifs de chaque classe. 

#effectif
table_Species<-table(iris$Species)

Table iris.png

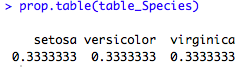
prop.table(table) permet d’obtenir les proportions au lieu des effectifs, pour une table déjà calculée. 

#proportion
prop.table(table_Species)

Proponevar iris.png

Représentation graphique

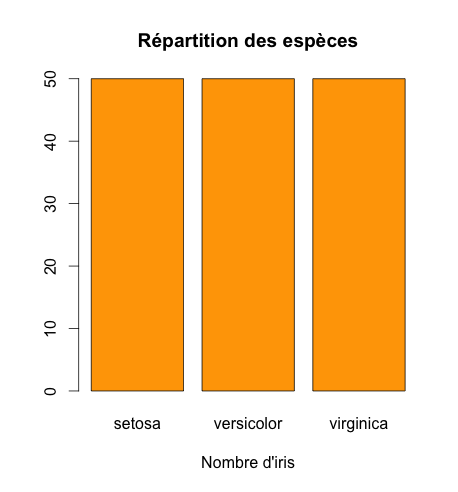
On peut représenter la table sous forme graphique avec un diagramme en bâtons (à ne pas confondre avec un histogramme !) 

#Barplot
barplot(table_Species, main="Répartition des espèces", 
        xlab="Nombre d'iris",
        col="orange")

Barplot iris.png


Statistiques bivariées :

L'objectif est de faire apparaître d'éventuelles liaisons entre deux variables X et Y décrivant une même population.

Deux variables quantitatives :

Statistiques

Un moyen d’évaluer l'intensité de la liaison entre deux variables est de calculer le coefficient de corrélation (linéaire) ou coefficient de corrélation de pearson.

<math> rho(X,Y)=\frac{cov(X,Y)}{sigmaX \times sigmaY} </math>

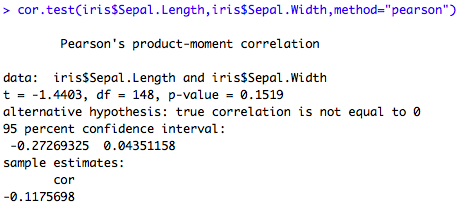
Ci dessous : le calcul du coefficient par la fonction cor(X,Y,method=« method"). 

## Coefficient de corrélation
cor(iris$Sepal.Length,iris$Sepal.Width,method="pearson")

Coeffcorr iris.png

Le test de corrélation peut aussi être directement effectué par la fonction cor.test(X,Y,method=« method").

H0 : corrélation entre les variables 

## test
cor.test(iris$Sepal.Length,iris$Sepal.Width,method="pearson")

Testcorr iris.png

Ici, on ne parvient pas à rejeter H0 (p-value>15%), i.e les deux variables sont effectivement corrélées.

Représentation graphique

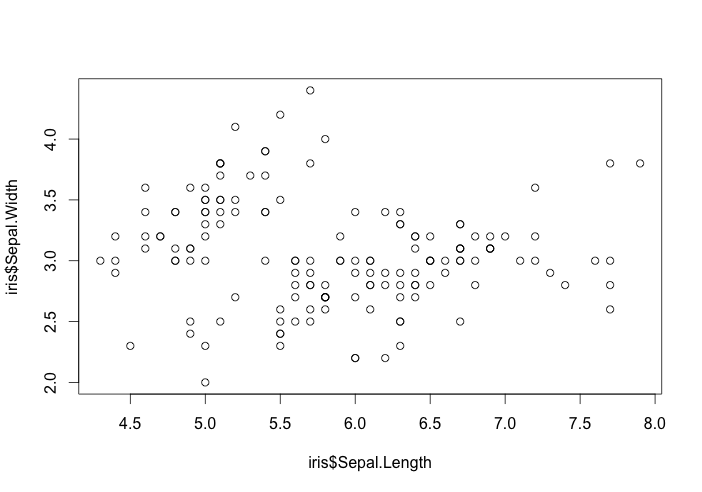
Graphiquement, on peut observer la dispersion (ou non) en représentant les observations dans un graphique avec la variable X en abscisse, et Y en ordonnées. La fonction plot dans son écriture la plus basique permet d’afficher le nuage de points : 

### scatterplot 
plot(iris$Sepal.Length,iris$Sepal.Width)

Scatterplot iris.png


Une quantitative, une qualitative

On étudie les caractéristiques de la variable quantitative (notée X), sur les sous-populations définies par les modalités de la variable qualitative (notée Y).

Statistiques

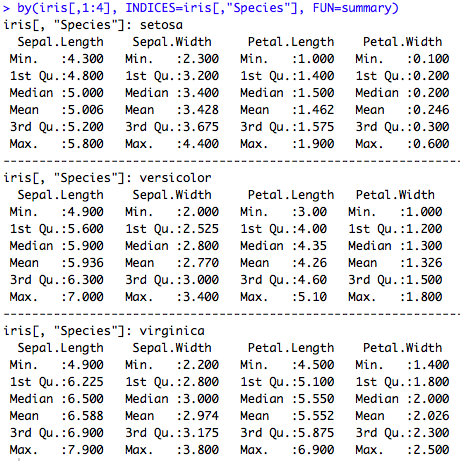
La fonction suivante permet de calculer des statistiques de base (fonction summary) par groupe (les groupes étant définis par les modalités d’une variable). Par exemple, ici des statistiques pour les iris de chaque espèce, séparément. 

###### descriptive statistics by group
by(iris[,1:4], INDICES=iris[,"Species"], FUN=summary)

By iris.png

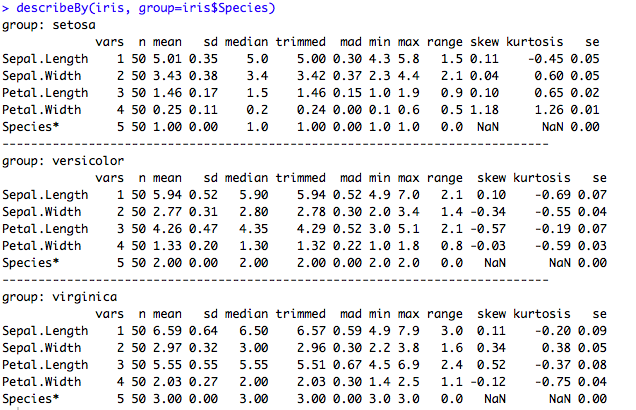
Le package « psych » permet de calculer les statistiques présentées par la fonction describe() (contenue par défaut dans R). Elles sont (dans l’ordre) :

  • Le nombre d’observations
  • la moyenne
  • l’écart-type
  • la médiane
  • la moyenne tronquée (calculée en enlevant les 5 plus petites et 5 plus grandes valeurs)
  • la déviation absolue à la médiane
  • le minimum
  • le maximum
  • l’étendue (minimum-maximum)
  • le coefficient d’assiymétrie (skew)
  • la Kurtosis
  • le standard error. 
## Package psych
install.packages("psych")
library(psych)
describeBy(iris, group=iris$Species)

Describeby iris.png

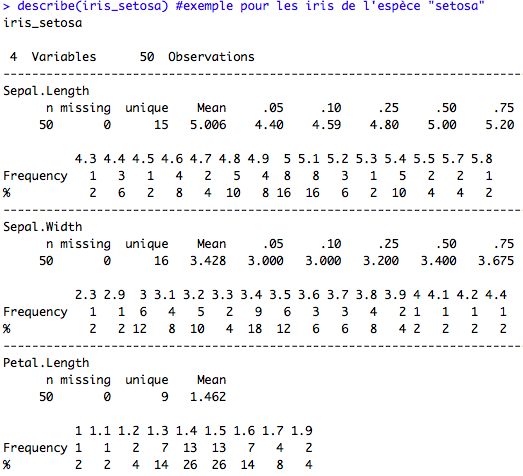
Il est aussi possible de réaliser des statistiques par groupe, par exemple en divisant la base de données selon la variable groupe, et en appliquant une des fonctions présentées précédemment sur le sous-jeu de données. Cependant, cette manière de procéder devient rapidement lourde dès lors qu’il y a un nombre important de facteurs pour la variable groupe. 

## A la main
iris_setosa<-iris[iris$Species=="setosa",colnames(iris)!="Species"] 
iris_versicolor<-iris[iris$Species=="versicolor",colnames(iris)!="Species"] 
iris_virginica<-iris[iris$Species=="virginica",colnames(iris)!="Species"] 
#
describe(iris_setosa) #exemple pour les iris de l'espèce "setosa"

Describemain iris.png

Représentation graphique

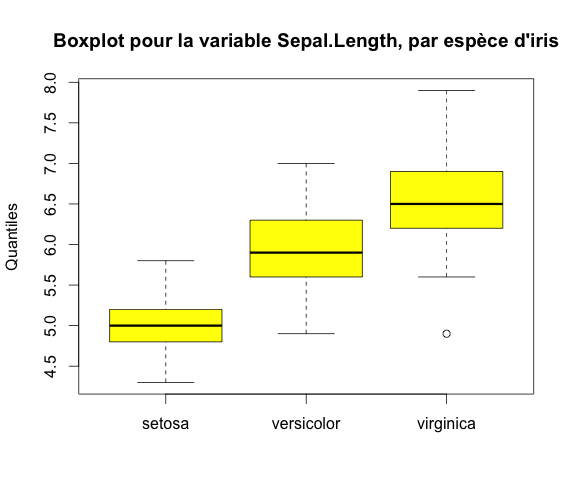
Graphiquement, on peut représenter des boxplots parallèles : pour une même variable X, pour chaque sous population (définie par la variable Y), avec la syntaxe : boxplot(variableX ~ variableY). 

## Une seule variable, par groupe
boxplot(iris$Sepal.Length ~ iris$Species,
        col = c("yellow"),
        main = paste("Boxplot pour la variable Sepal.Length, par espèce d'iris"),
        ylab = "Quantiles")

Boxplotparralleles iris.png

Test

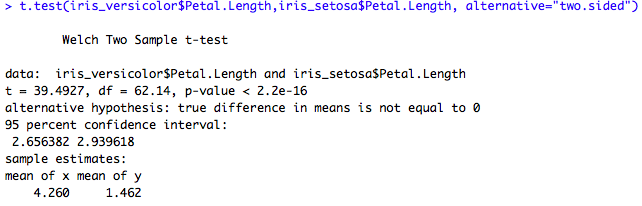
On peut vouloir tester si la longueur des pétales des iris de l'espèce "setosa" est significativement différente (au sens statistique du terme) de celle des pétales de l'espèce "versicolor". Pour celà, on effectue un test de Student.

H0 : Différence non significative (i.e nulle) 

#Test de Student
t.test(iris_versicolor$Petal.Length,iris_setosa$Petal.Length)

Ttest iris.png

La p-value étant quasiment nulle, on rejète fortement H0. Cela signifie qu'il existe bien une différence significative entre la taille des pétales d'iris de ces deux espèces.

De manière plus générale, on peut vouloir tester si la longueur des pétales des Iris diffère de manière significative entre les fleurs de différentes espèces (pour les trois espèces représentées dans la base de données). Pour cela, on réalise une ANOVA.

H0 : Différence non significative 

# ANOVA
anova <- aov(Petal.Length ~ Species, data=iris)
anova
summary(anova)

Anova.png

La p-value étant quasiment nulle, on rejète fortement H0. Cela signifie qu'il existe bien une différence significative entre la taille des pétales d'iris de deux espèces différentes (parmi les trois espèces des données).

Deux variables qualitatives :

La base de données utilisée ne contenant qu'une seule variable qualitative, on en crée une seconde, afin de pouvoir illustrer la suite par des exemples. Fictive, cette variable est basée sur la variable Sepal.Length et prend au choix la valeur « petite » (Sepal.Length<=5), « moyenne » (Sepal.Length>5 mais <=6) ou « grande »(Sepal.Length>6), pour chaque observation. 

## On crée une nouvelle variable facteur : 
iris$Sepal.Length_cat[iris$Sepal.Length<=5]<-"petit"
iris$Sepal.Length_cat[iris$Sepal.Length<=6 & iris$Sepal.Length>5]<-"moyen"
iris$Sepal.Length_cat[iris$Sepal.Length>6]<-"grand"

Tableau

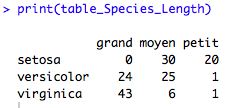
On peut résumer ici les effectifs sous la forme d’un tableau à double entrée, toujours avec la fonction table, avec la syntaxe suivante : table(variable1,variable2,……variablen). A noter que le nombre de variables n’est pas limité à deux. 

## Table
table_Species_Length<-table(iris$Species,iris$Sepal.Length_cat)
print(table_Species_Length)   #pour afficher le tableau

Tablequali iris.png

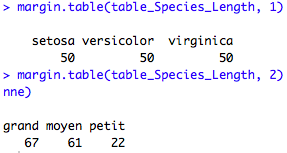
On peut également obtenir les effectifs totaux, par ligne ou par colonne grâce à la fonction margin.table(table). Par exemple ci dessous, il y a 50 iris de chaque espèce (toutes tailles confondues), et il y a 67 iris répertoriés comme « grand », toutes espèces confondues. 

## Effectifs totaux
margin.table(table_Species_Length, 1) ## Effectifs pour chaque classe de la variable Species (ligne)
margin.table(table_Species_Length, 2) ## Effectifs pour chaque classe de la variable Length_cat (colonne)

Margin iris.png

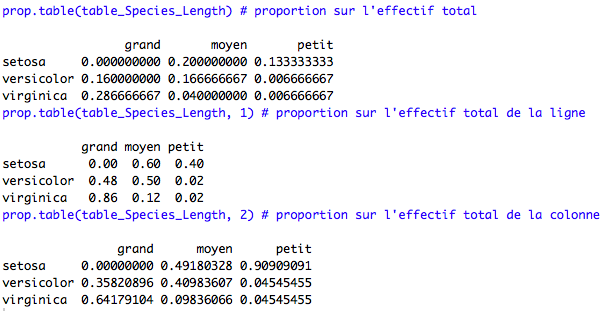
La fonction prop.table(table) permet d’obtenir les proportions totales, par ligne, et par colonne. 

### Proportions
prop.table(table_Species_Length) # proportion sur l'effectif total
prop.table(table_Species_Length, 1) # proportion sur l'effectif total de la ligne
prop.table(table_Species_Length, 2) # proportion sur l'effectif total de la colonne

Proptable iris.png

Le package gmodels permet de réaliser des tableaux plus élaborés (semblables aux tableaux PROC FREQ dans SAS). Le contenu des cellules est présenté en haut à gauche. 

######## Package gmodels
install.packages("gmodels")
library(gmodels)
CrossTable(iris$Species,iris$Sepal.Length_cat,prop.chisq=FALSE,chisq=FALSE,expected=FALSE)


Test d’indépendance

Deux variables qualititatives X et Y sont indépendantes si les effectifs de chaque modalité de la variable X sont significativement différents pour chaque modalité de la variables Y. Le test d’indépendance est basé sur le test du Khi-Deux, accessible directement par la fonction chisq.test(x,y), ou par l’option chisq=TRUE dans la fonction CrossTable (voir précédemment).

A noter que pour être appliqué, il est nécessaire d'avoir au minimum 5 observations au sein de chaque classe (critère de Cochrane).

H0 : Indépendance entre les variables Si la p-value est inférieure à \alpha, alors on rejète H0 ; à savoir que les variables ne sont pas indépendantes (ce qui est le cas ici). 

### Test d'indépendance du Chi-Deux
chisq.test(iris$Species,iris$Sepal.Length_cat)

Testkhideux iris.png


A noter que le package gmodels permet d’inclure dans le tableau déjà présenté ci-dessus les effectifs attendus en cas d’indépendance entre les variables (sur lesquels se base la statistique du Khi-Deux). Pour plus de lisibilité, on a supprimé l’affichage dans le tableau des proportions par cellule, par ligne et par colonne, pour ne garder que (dans l’ordre) : l’effectif réel, l’effectif attendu si indépendance et la contribution de chaque cellule à la statistique du Khi-Deux. 

#Expected counts et effectifs réels
library(gmodels)
CrossTable(iris$Species,iris$Sepal.Length_cat,prop.t=FALSE,prop.c=FALSE,prop.r=FALSE,prop.chisq=TRUE,chisq=TRUE,expected=TRUE)

Tablekhi iris.png

Récupérée de « https://odr.inra.fr/intranet/carto/cartowiki/index.php?title=Statistiques_descriptives_avec_R&oldid=15786 »