Regression linéaire avec R

Données

Pour illustrer, on utilise le jeu de données « housingprices » (issu du package DAAG), composé de quinze observations et trois variables :

• sale.price = prix de vente de la maison (en milliers de dollars australiens)
• area = surface au sol de la maison
• bedrooms = nombre de chambres dans la maison

#### Package DAAG
install.packages("DAAG")
library(DAAG)

head(houseprices)

Objectif

On peut vouloir expliquer le prix de vente des maisons, en fonction de leur surface en présumant que plus la surface est élevée, et plus le prix de vente sera élevé. Il s'agit là d'une regression dite "simple" car elle ne comporte qu'une seule variables explicative. De plus, on peut aussi supposer que le nombre de chambres influence le prix de la maison à la hausse ; il s'agira là d'une regression "multiple" avec deux variables explicatives.

L’objectif est d’évaluer si chacune des deux variables influence le prix, et, si tel est le cas, de tenter de quantifier cet effet.

La regression linéaire

La regression linéaire assume que la relation entre les variables explicatives et la variable à expliquer va être linéaire, du type : <math>y_{i} = b0 + b1 \times x1_{i} + b2 \times x2_{i} + e_{i} </math>

où :

• y est la variable à expliquer (ici : sale.price)
• x1 et x2 sont les variables explicatives (ici : la surface et le nombre de chambres)
• e est le terme d’erreur, assumé être distribué selon une loi Normale : <math>e_i \rightarrow \mathcal{N}(0,\sigma^2) </math>.

Sous un certain nombre d'hypothèses, la méthode des moindres carrés ordinaires (OLS pour Ordinary Least Square) permet d'obtenir des estimateurs BLUE (Best Linear Unbiased Estimators), c'est-à-dire qui sont sans biais et à variance minimale. Les coefficients estimés sont issus de la minimisation de la somme des carré des résidus entre les valeurs prédites et les valeurs observées,formellement : <math> (\hat{b0} ; \hat{b1}) = \underset{\hat{b0},\hat{b1}}{argmin} \sum_{i=1}^{n} \hat{e_i}^2 = \underset{\hat{b0},\hat{b1}}{argmin} \sum_{i=1}^{n} (y_i - \hat{b0} - \hat{b1} \times x1_i - \hat{b2} \times x2_i) ^2 </math>

Regression linéaire simple

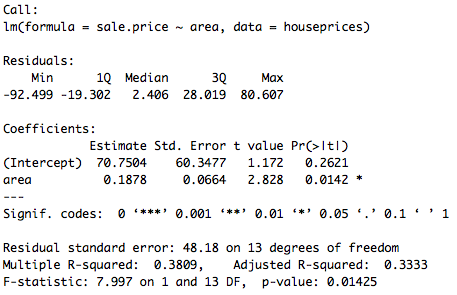
Dans ce cas, on considère une seule variable explicative. Ici, on souhaite donc estimer les coefficients du modèle :<math> sale.price = b0 + b1 \times area + e </math> La commande à utiliser dans R est : lm()

# y = b0 + b1*x1
# Variable à expliquer : y = prix de vente de la maison
# Une variable explicative : x1 = Surface au sol de la maison

pricereg<-lm(sale.price ~ area, data=houseprices)

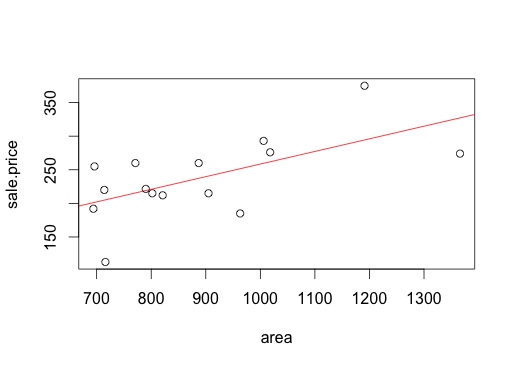
On a donc l'équation de la droite de régression : <math> sale.price= 70.75 + 0.188 \times area + \hat{e} </math> , que l'on peut tracer avec le nuage de points :

# plot : "vraies" valeurs et droite de regression
plot(sale.price ~ area, data=houseprices)
abline(pricereg, col = "red") 

Regression linéaire multiple

Ici, on considère deux (ou plus) variables explicatives. On souhaite donc estimer les coefficients du modèle : <math> sale.price = b0 + b1 \times area + b2 \times bedroom + e </math>

# Variables explicatives : x1 = Surface au sol de la maison, x2 = nombre de chambres
pricereg2<-lm(sale.price ~ area + bedrooms , data=houseprices)

Interprétation

L'équation de la droite de regression est : <math> sale.price = -141.76 + 0.14 \times area + 58.32 \times bedrooms </math>. Les coefficients associés aux variables "area" et "bedrooms" sont significatifs (respectivement à 95% et à 99%, cf : sortie précédente), on peut donc les interpréter. Toutes choses égales par ailleurs, une chambre supplémentaire augmente par exemple le prix de la maison de 58 milles dollars environ, et 100 unités de surface (inconnue) supplémentaires vont l’augmenter de 14 mille dollars, toutes choses égales par ailleurs.

Fonctions

summary

summary() permet de produire les sorties pour chaque regression présentées précédemment. Ainsi, cette fonction affiche : les coefficients estimés, leur écart-type, et la valeur de la statistique t de Student ainsi que la p-value (probabilité que le coefficient soit significativement différent de zéro) associées à chaque coefficient. Sont aussi présentés le R2 et R2 ajusté, ainsi que la statistique F de Fisher (testant la significativité globales des variables), son degré de liberté, et la p-value associée.

#### Regression output
summary(pricereg2)

Coefficient

coef() permet de n’extraire que les coefficients estimés.

#### Extraction des coefficients
coef(pricereg2)

Confint

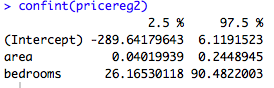
confint() permet d’afficher l’intervalle de confiance à 95% pour les coefficients estimés.

#### Intervalle de confiance (à 95%) des coefficients
confint(pricereg2)

Residuals

resid() permet d’extraire les résidus.

#### Extraction des résidus
resid(pricereg2)

Fitted

fitted() permet d’extraire les valeurs prédites.

#### Extraction des valeurs prédites
fitted(pricereg2)

Predict

La fonction predict() permet de prédire la valeur de y (i.e du prix) pour de nouvelles données (des variables explicatives). Seul les deux premiers arguments sont requis : se.fit permet d’afficher l’écart-type de la valeur prédite, et interval et level permettent afficher ici les valeurs de l’intervalle de confiance fixé à 99%.

#### Prédiction du prix de la maison en fonction de sa superficie et de son nombre de chambres
predict(pricereg2, newdata=data.frame(area=800,bedrooms=2), se.fit=TRUE, interval = "prediction", level = 0.99)

Ainsi, le prix estimé d’une maison dont la surface au sol est de 800 unités et qui a 2 chambres serait de 88.92 mille dollars.