Modèle linéaire généralisé avec R

Définition

Il s'agit de modèles linéaires plus souple que le modèle linéaire "traditionnel", qui vont être utiles lorsque la variable à expliquer n’est pas une variable quantitative continue. En effet, le modèle linéaire général ne convient pas pour certaines variables à expliquer, comme par exemple pour les données de comptage ou pour les probabilités.

Par exemple, les valeurs prédites peuvent en effet n’être pas entière (pour les données de comptage) ou hors de l’intervalle [0,1] (pour une probabilité).

En outre, le modèle linéaire général repose sur l’hypothèse de normalité du terme d’erreur, et la variable à expliquer y est ainsi aussi considérée comme distribuée normalement (hypothèse très forte). (voir Regression linéaire avec R). Or, il paraît souvent abusif de considérer la variable à expliquer (et son erreur) comme suivant une loi normale puisque cela supposerait une distribution symétrique (alors que par exemple ce n’est très probablement pas le cas pour des données de comptage).

Enfin, avec l’hypothèse d’espérance nulle du terme d’erreur, on a : <math> E(y/x) = b0+b1 \times x1+b2 \times x2. </math>
Le modèle linéaire général considère ainsique les effets des variables explicatives sur la variable à expliquer sont linéaires, ce qui n’est très souvent pas le cas.

Le modèle linéaire généralisé considère plutôt une relation du type : <math> E(y/x)= g(b0+b1 \times x1+b2 \times x2) </math>

La fonction inverse de g(...), est appelée la fonction de liaison, et prend la forme : <math>f(E(y/x)) = b0 + b1 \times X1 + b2 \times X2 + ... + bk \times Xk </math>

Enfin, le modèle linéaire généralisé va tenir compte de la non-normalité du terme d’erreur, et choisir une autre distribution pour la modéliser.

La fonction GLM()

Généralités

La fonction glm() est utilisée dans R, avec la syntaxe générale : glm(formula, family=familytype(link=linkfunction), data=dataset)

où :

• formula est la formule classique pour écrire le modèle à estimer (de type : y ~ x1 + x2 + ...) où y est la variable à expliquer et x1,x2,... sont les variables explicatives.
• family représente la distribution du terme d’erreur et link la forme de la fonction lien spécifiée.

Quelques exemples :

?family

• binomial(link = "logit") #Modèle LOGIT
• gaussian(link = "identity")
• Gamma(link = "inverse")
• inverse.gaussian(link = "1/mu^2")
• poisson(link = "log")
• quasi(link = "identity", variance = "constant")
• quasibinomial(link = "logit")
• quasipoisson(link = "log")

A noter que family=« gaussian » renvoie à la fonction lm et au modèle linéaire général puisque la fonction de lien est l’identité. Parmi les modèles les plus utilisés on trouve :

• le modèle LOGIT et PROBIT (lorsque la variable à expliquer est de type binaire (typiquement 0-1), et que l’on cherche à expliquer une probabilité : par exemple la probabilité pour un composant d’être défectueux…
• le modèle de Poisson, utilisé pour des données de comptage (ex : nombre de visites chez le médecin, nombre de buts marqués,...).

Modèle LOGIT et PROBIT :

Présentation

Il est sont l’un des usages les plus courants de la fonction glm(). Il sont utilisés lorsque la variable à expliquer est de type binaire, et que les variables explicatives sont continues ou binaires. Tous deux utilisent une loi binomiale (family).

<math> Y=g(b0+b1 \times x1 +b2 \times x2 +....)</math>

L'inverse de la fonction de lien (notée g précédemment) peut être une loi logistique (ce qui donne un modèle LOGIT) ou celle de la loi Normale centrée réduite (modèle PROBIT). A noter que le modèle LOGIT est aujourd’hui le plus utilisé (l’avantage initial du PROBIT était la fonction de lien plus « simple » à calculer à la main, ce qui n’est plus important aujourd’hui avec l’utilisation de logiciels).

Application : modèle

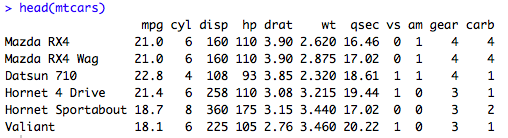
Pour illuster, on utilise le jeu de données contenu dans R : mtcars, qui contient 32 observations et 11 variables, dont 3 variables qui vont nous intéresser :

• am : La voiture est-elle dotée d'une boîte de vitesse manuelle ?
• hp : nombre de chevaux
• wt : poids

## On charge le jeu de données :
data(mtcars)
## On observe les premières lignes de la base de données
head(mtcars)

On souhaite déterminer si la probabilité pour une voiture d’être dotée d’une boîte à vitesses manuelle (variable am) dépend où non du nombre de chevaux (variable hp) et de son poids (variable wt). On a un exemple ici où le modèle linéaire général peut produire une valeur estimée de cette probabilité (p=E(am/wt,hp)) ou des effets marginaux hors de l’intervalle [0,1].

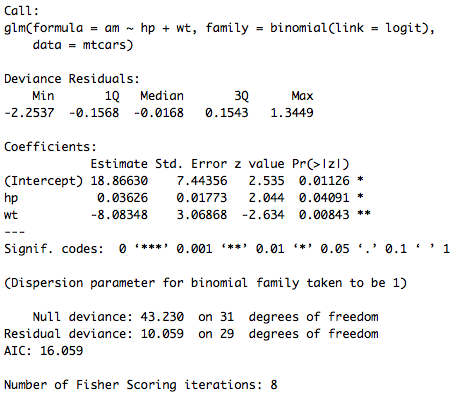
##### LOGIT

regLOGIT=glm(am ~ hp + wt, data=mtcars, family=binomial(link=logit))
summary(regLOGIT)

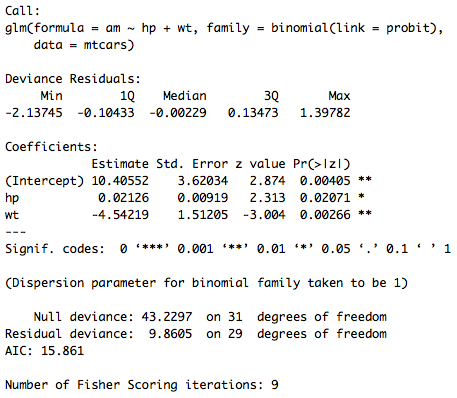
##### PROBIT

regPROBIT=glm(am ~ hp + wt, data=mtcars, family=binomial(link=probit))
summary(regPROBIT)

Fonction (affichage, extraction,..)

Les fonctions présentées pour la fonction lm() (voir : Regression linéaire avec R) sont aussi valables pour la fonction glm(), à savoir pour les plus utilisées :

• summary() pour afficher la sortie complète
• coef() pour extraire les coefficients
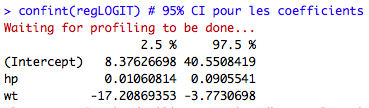
• confint() pour extraire leur intervalle de confiance (à 95%)
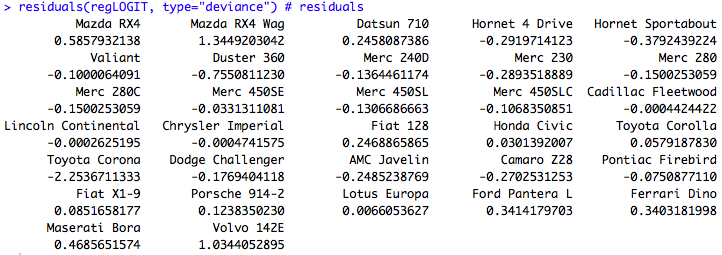
• fitted() pour extraire les valeurs estimées
• resid() pour extraire les résidus.

Comme le modèle est estimé par maximum de vraisemblance, il peut être utile d’extraire la vraisemblance du modèle, avec la fonction logLik() (NB : Cela est aussi possible pour un objet de classe lm, mais peu utilisé)

#vraissemblance
logLik(regLOGIT)

Interprétation

De plus, bien que possible, il n’est pas d’usage d’interpréter les coefficients de tels modèles. En raison de la fonction qui définit la relation entre la variable à expliquer et les variables explicatives, les coefficients présentés dans le tableau précédent n’ont pas de signification en eux-mêmes (sans transformation) :

Variable continue

En effet, pour le logit la fonction de lien utilisée étant une fonction logistique, on a : <math> f(y)=log(\frac{p}{1-p})=18.87+0.036 \times hp-8.08 \times wt </math>
où p = E(am/X) = probabilité pour la voiture d'être dotée d'un boîte de vitesses manuelles (P(am)=1).

Une autre manière de l'écrire est en utilisant la fonction g (inverse de la fonction lien f) : <math>E(am/X)=g(18.87+0.036 \times hp-8.08 \times wt) </math> avec g la fonction de répartition de la loi logistique pour le LOGIT (le raisonnement est le même en utilisant la fonction de répartition de la loi Normale centrée réduire pour le PROBIT par exemple ou de n'importe quelle loi associée à un modèle). Pour simplifier pour la suite, on note <math> E(am/X)=g(X'b). </math>

On a donc l'effet marginal de la variable <math> x_{j} </math> (qui peut être wt ou hp)  : <math> \frac{\partial E(am/X)}{\partial x_{j}} = \frac{\partial g(X'b)}{\partial X'b } \times \frac{\partial X'b}{\partial x_{j}} = f(X'b) \times b_{j}</math>
où f est la fonction de densité de la variable (i.e la fonction lien, ici logistique).

On constate que l'effet marginal de la j-!ème variable (i.e le coefficient associé à la j-ième variable) va dépendre des valeurs prises par l'ensemble des variables explicatives, et pas seulement de la valeur prise par la variable concernée. Il est d'usage de prendre alors des valeurs moyennes pour les autres variables.

Par exemple, ci-dessous on calcule l'effet marginal associé à la variable nombres de chevaux (pour un poids moyen de la voiture)

##interprétation
#continue
xavg<-c(1,mean(mtcars$hp),mean(mtcars$wt)) # intercept, valeur moyenne pour hp, valeur moyenne pour wt 
betaLOGIT<-coefficients(regLOGIT)
betaLOGIT_hp<-betaLOGIT[2] # Coeff associé à hp

MEhp=betaLOGIT_hp*dlogis(betaLOGIT%*%xavg)
print(MEhp) #0.0043

10 chevaux en plus sur la voiture augmente donc la probabilité d'avoir une boîte manuelle de 4,3 points de pourcentage, toutes choses égales par ailleurs, et pour une voiture ayant un poids moyen.

Variable dichotomique

On considère un individu avec des observations moyennes pour les variables explicatives. L'effet marginal va ici être la différence de probabilité entre la probabilité de cette individu lorsque la variable dichotomique <math> x_{j} </math> prend la valeur 1, et sa probabilité lorsque cette variable prend la valeur 0.

Formellement : <math> E(y/X, x_{j}=1)-E(y/X, x_{j}=0) </math>.

Pour illustrer, on introduit une troisième variable dans la régression (variable vs), qui elle est binaire. La variable vs prend la valeur 1 s'il s'agit d'un moteur de type "V-engine", et 0 s'il s'agit d'un moteur de type "straight engine".

#dummy
regLOGIT3=glm(am ~vs+ hp + wt, data=mtcars, family=binomial(link=logit))

betaLOGIT3<-coefficients(regLOGIT3)

x1<-c(1,1,mean(mtcars$hp),mean(mtcars$wt)) # vs=1
x0<-c(1,0,mean(mtcars$hp),mean(mtcars$wt)) # vs=0

p1<-plogis(betaLOGIT3%*%x1) #proba si vs=1
p0<-plogis(betaLOGIT3%*%x0) #proba si vs=0

MEvs=p1-p0 #Effet marginal

print(MEvs) #baisse de 26,5 pts de pourcentage

Avoir un moteur de type "V-engine" augmente donc la probabilité pour la voiture d'avoir une boîte manuelle de 26,5 points de pourcentage comparé à une voiture ayant un moteur de type "straight engine" ; toutes choses égales par ailleurs, et pour une voiture ayant un poids et un nombre de chevaux moyens.

Prédiction

En revanche, il est beaucoup plus facile d'utiliser le modèle pour la prédiction :

##Prédiction (modèle logit) :
predict(regLOGIT, newdata=data.frame(hp=100,wt=2.88), type="response")

Une voiture avec une puissance de 100 chevaux et un poids de 2.88 lb/1000 va donc avoir une probabilité estimée d’être équipée d’une boîte manuelle de 31% environ.

Modèle de Poisson

Il est utilisé pour des données de type comptage (exemple : nombre de visites chez le médecin, etc), dont la distribution ressemble plus à une distribution de Poisson qu’à une Normale (par exemple). En effet, les caractéristiques de ce type de données sont : d’être discrètes, d'avoir une forte fréquence pour de faibles modalités, et de ne pas pouvoir prendre de valeurs négatives.

Application

### On charge le package AER
library(AER)

### On charge les données
data(RecreationDemand)

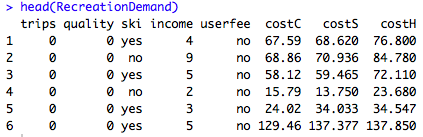
Le jeu de données utilisé en exemple est « RecreationDemand » contenu dans le package « AER » (à charger au préalable ». Il est composé de 659 observations basée sur un sondage administré à 2000 propriétaires (enregistrés) de bateaux de plaisance dans 23 comtés de l’est du Texas. Il compte 8 variables :

• trips : Le nombre d’excursions en voilier (trips)
• quality : La qualité du service (sur une échelle de 1 à 5)
• ski : est-ce que la personne est inscrite au water-skiing sur le lac ?
• userfee : Et-ce qu’il paye une taxe annuelle au lac Somerville?
• costC : Dépenses (en dollars) quand il a visité le lac Conroe
• costS : Dépenses (en dollars) quand il a visité le lac Somerville
• costH : Dépenses (en dollars) quand il a visité le lac Houston

On souhaite expliquer le nombre d’excursions en fonction des autres variables. Comme il s’agit de données de comptage, on utilise le modèle de Poisson :

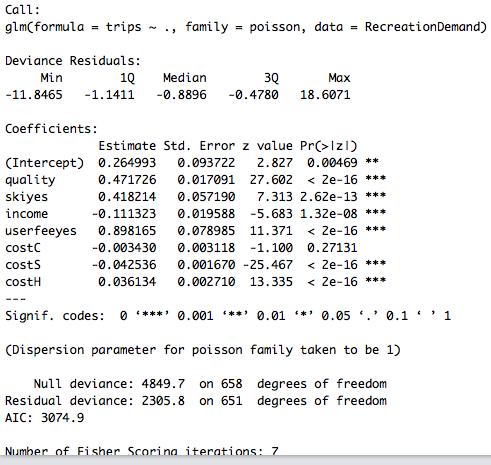
## Modèle de Poisson
#variable à expliquer = nombre de voyages, variables explicatives : les 7 autres de la base de données
Reg_pois <- glm(trips ~ ., data = RecreationDemand, family = poisson)
summary(Reg_pois)

La fonction de lien étant la fonction log(), on a : <math> log(y) = 0.26 + 0.4717 \times quality +</math> ... <math>+ 0.036 \times costH. </math>

De nouveau predict() va permettre d’estimer le nombre d’excursion pour un propriétaire de bateaux donné (i.e avec des valeurs données pour les variables). <math> y_{predict} = exp(0.26 + 0.4717 \times quality_{predict} +</math> ... <math>+ 0.036 \times costH_{predict}) </math>

De même, on peut aussi extraire la vraissemblance du modèle :

Overdispersion

En assumant que la variable à expliquer suit une loi de Poisson, cela implique que la moyenne est égale à sa variance. Or, dans de nombreux cas, la variance est plus élevée, on parle d’overdispersion. L'utilisation d’un modèle de Poisson va alors conduire à une sous-évaluation de la variance, et donc une sur-évaluation des statistiques de test (dont le calcul inclue bien souvent une division par l’écart-type), et donc finalement va conduire à rejeter l’hypothèse nulle plus souvent qu’il ne le devrait.

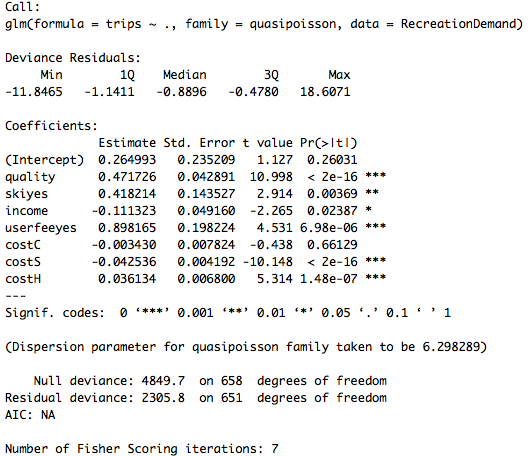
Dans ce cas, il est d’usage d’utiliser family=« quasipoisson » plutôt que « poisson ». La différence est que avec quasi poisson le paramètre de dispersion n’est plus fixé à 1 (dans l'exemple, il va être de 6.3 environ : cf infra). De plus, es coefficients estimés vont être inchangés, mais leurs écart-type vont être corrigés (et avec les statiques de test et p-value associées) pour tenir compte de ce phénomène d’overdispersion, comme le montrent les résultats ci-dessous.

#Quasi Poisson
Reg_quasipois <- glm(trips ~ ., data = RecreationDemand, family = quasipoisson)
summary(Reg_quasipois)